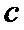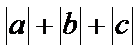- 利用基本不等式求最值
- 共114题
10. 已知(
正确答案
解析








故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
含x2与x3的项的系数,再根据绝对值之比为1:6,算得
易错点
确定项的系数时计算易出错。
知识点
15.设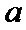
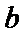
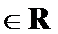
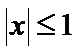
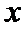
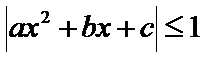
的最大可能值为______.
正确答案
3
解析
任意满足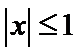
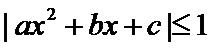
即有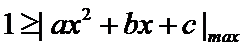
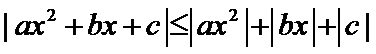
由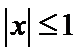
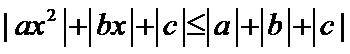
可得当且仅当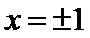
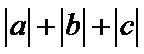
即有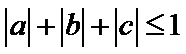
即有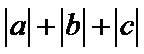
故答案为:1.
考查方向
解题思路
由题意可得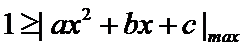
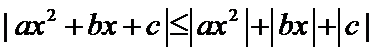
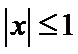
易错点
主要易错于不等式的转化,
知识点
14.若

正确答案
解析
由基本不等式得



考查方向
解题思路
利用基本不等式得到
易错点
找不到

知识点
7. 若不等式


正确答案
解析
由基本不等式得
(1)当



(2)当






(3)当







考查方向
解题思路
1.先利用基本不等式将题中给出的不等式转化为
2.利用分类讨论的思想求解出k的取值范围。
易错点
1.不知道分类的标准导致出现混乱;
2.不会分离常数求参数的取值范围。
知识点
9.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c,


正确答案
解析
由题意可知 


考查方向
解题思路
根据题意可求3a+2b的值,然后构造基本不等式的形式求解问题答案
易错点
计算错误,活用“1”
知识点
扫码查看完整答案与解析