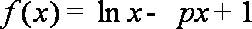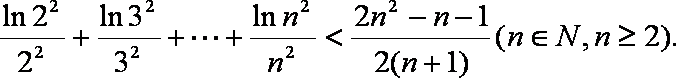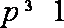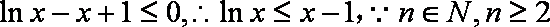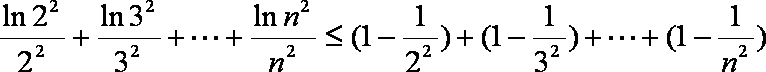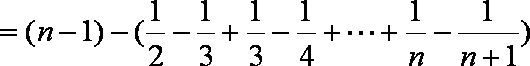- 不等式与函数的综合问题
- 共21题
选修45:不等式选讲
正确答案
见解析
解析
知识点
已知函数


(1)讨论
(2) 若不等式

(3)若方程


正确答案
见解析。
解析
(1)

其导数
①当


②当



所以,

(2)当



能使

当

问题化为求

由于







即

(3)由于



构造函数:

所以函数



于是





知识点
设函数
(1)求函数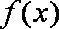
(2)当p>0时,若对任意的x>0,恒有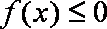
(3)证明:
正确答案
见解析
解析
(1)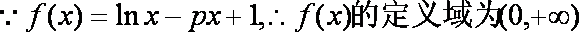
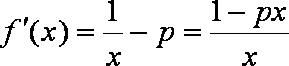
当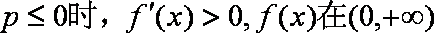

当p>0时,令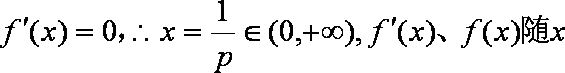
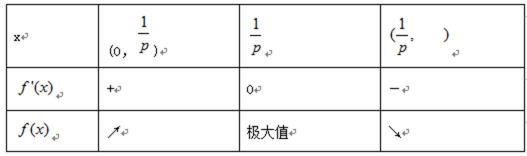
从上表可以看出:当p>0 时,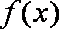
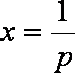

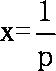
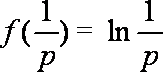
要使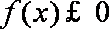
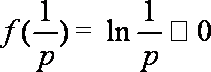
∴p的取值范围为[1,+∞
(3)令p=1,由(2)知,
∴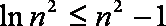
∴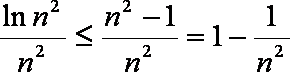
∴

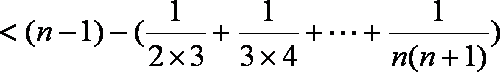
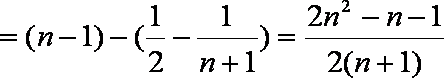
∴结论成立
知识点
已知等差数列






(1)求数列

(2)设数列




正确答案
见解析
解析
(1)有题可知a2+ a5= 2,a2a2=27又因为d>0,所以a2=3 a5=9,d=2
an=2n-1
又因为

数列{bn}为等比数列,
(2) Sn=n2 Sn+1=(n+1)2,
=
猜想,当n》4时,
证明:n=4时成立
假设n=k时成立,即
当n=k+1时,
由上可知当n》4时,
知识点
3.不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析