- 利用基本不等式求最值
- 共114题
6.正项等比数列{an}中,存在两项am、an使得

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某工厂生产某种产品,每日的成本C(单位:元)与日产里



已知每日的利润


(Ⅰ)求
(Ⅱ)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
解:(Ⅰ)由题意可得:
解析
解析已在路上飞奔,马上就到!
知识点
8.已知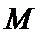
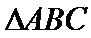
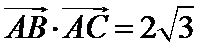
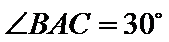
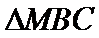
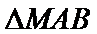
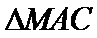
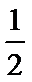
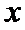
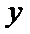
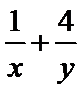
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.有一种变压器铁芯的截面呈如图所示的正十字形,为保证所需的磁通量,要求正十字形的面积为4
正确答案
设外接圆半径为R,AB =x(0<x<R),DG =y,则4R2=x2+y2 (1),
由已知条件有2xy-x2=4

代入(1)得4R2= x2 +
∴4R2=

当且仅当
代入(2)得y=1+
∴当 x=2 且y=1+
此时正十字形外接圆周长最短。
答:正十字形的长和宽分别为(1+
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,海上有






(1)用



(2)晚上小艇在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得

(1)若广告商要求包装盒侧面积S(cm

(2)若广告商要求包装盒容积V(cm


正确答案
解:(1)由题意知, 包装盒的底面边长为







(2)包装盒容积V=

所以





所以当



解析
解析已在路上飞奔,马上就到!
知识点
20.为了提高产品的年产量,某企业拟在2014年进行技术改革,经调查测算,产品当年的产量




(1)试确定


(2)该企业2014年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获利5万元,每吨乙产品可获
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



















