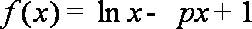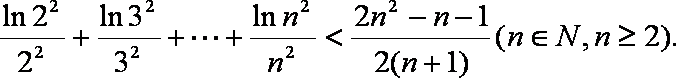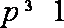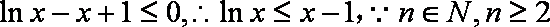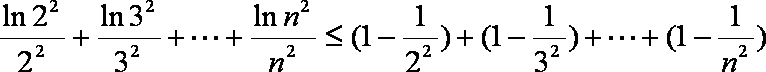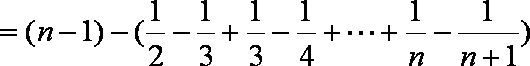- 不等式与函数的综合问题
- 共21题
已知函数
25.若函数


26.令





27.当
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
19.已知函数

(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a
正确答案
(1)详见解析;(2)3;
解析
试题分析:(1)分析题意可知





(1)由f(x)= 














(2)由M(a,b)








考查方向
解题思路
(1)根据a的取值范围,得到函数在[-1,1]上的单调性,分类讨论证得结论;(2)由题中给出的新定义进行求解.
易错点
二次函数在闭区间上的单调性.
知识点
21.已知函数
(I)若函数


(II)证明:
(III)若不等式

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
1)根据共同的切线的理解得到该点处导函数值与函数值都相等得到t
2)利用单调性确定绝对值内的正负,去掉绝对值号,利用
3)构造关于m的一次函数,把x当作参数消掉m后再使用恒成立问题的解答得出结果
易错点
本题易错在以下几个方面
1)对共同的切线理解不足,第一问出错
2)不能有效去掉绝对值,使用错的解题思想
3)变量间关系不能有效理清
知识点
2. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.关于x的不等式:
正确答案
–1<x<2
解析
解析已在路上飞奔,马上就到!
知识点
选修45:不等式选讲
正确答案
见解析
解析
知识点
已知函数


(1)讨论
(2) 若不等式

(3)若方程


正确答案
见解析。
解析
(1)

其导数
①当


②当



所以,

(2)当



能使

当

问题化为求

由于







即

(3)由于



构造函数:

所以函数



于是





知识点
设函数
(1)求函数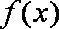
(2)当p>0时,若对任意的x>0,恒有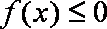
(3)证明:
正确答案
见解析
解析
(1)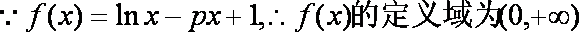
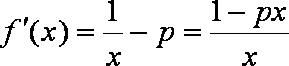
当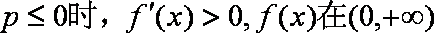

当p>0时,令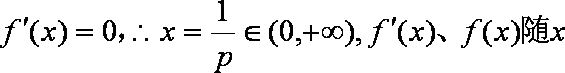
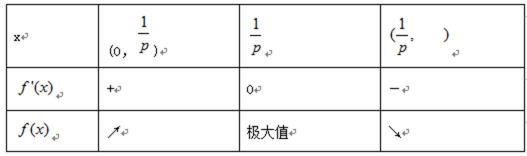
从上表可以看出:当p>0 时,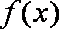
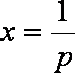

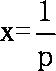
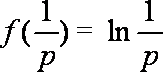
要使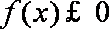
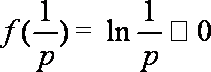
∴p的取值范围为[1,+∞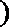
(3)令p=1,由(2)知,
∴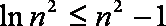
∴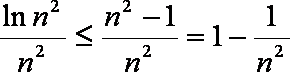
∴

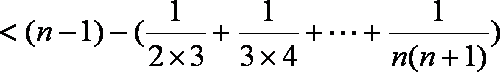
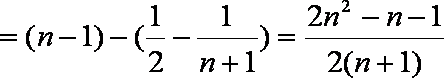
∴结论成立
知识点
已知等差数列






(1)求数列

(2)设数列




正确答案
见解析
解析
(1)有题可知a2+ a5= 2,a2a2=27又因为d>0,所以a2=3 a5=9,d=2
an=2n-1
又因为

数列{bn}为等比数列,
(2) Sn=n2 Sn+1=(n+1)2,
=
猜想,当n》4时,
证明:n=4时成立
假设n=k时成立,即
当n=k+1时,
由上可知当n》4时,
知识点
3.不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析