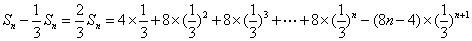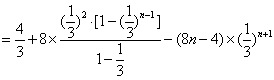- 错位相减法求和
- 共37题
已知各项均为正数的数列{an}前n项和为Sn,(p – 1)Sn = p2 – an,n∈N*,p > 0且p≠1,数列{bn}满足bn = 2logpan。
(1)求an,bn;
(2)若p =

(3)是否存在自然数M,使得当n > M时,an > 1恒成立?若存在,求出相应的M;若不存在,请说明理由。
正确答案
见解析。
解析
(1)由(p – 1)Sn = p2 – an (n∈N*) ①
由(p – 1)Sn – 1 = p2 – an – 1 ②
① – ②得
∵an > 0 (n∈N*)
又(p – 1)S1 = p2 – a1,∴a1 = p
{an}是以p为首项,
an = p
bn = 2logpan = 2logpp2 – n
∴bn = 4 – 2n
(2)证明:由(1)知,bn = 4 – 2n,an = p2 – n
又由条件p =
∴Tn =

① – ②得
= 4 – 2 ×
= 4 – 2 ×
∴Tn =
Tn – Tn – 1 =
当n > 2时,Tn – Tn – 1< 0
所以,当n > 2时,0 < Tn≤T3 = 3
又T1 = T2 = 4,∴0 < Tn≤4。
(3)解:若要使an > 1恒成立,则需分p > 1和0 < p < 1两种情况讨论
当p > 1时,2 – n > 0,n < 2
当0 < p < 1时,2 – n < 0,n > 2
∴当0 < p < 1时,存在M = 2
当n > M时,an > 1恒成立。
知识点
已知函数


(1)求数列
(2)设


正确答案
见解析。
解析
(1)由题意得



(2)由(1)得


①-②得


设
得




又

知识点
已知数列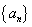
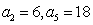
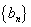
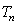
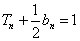
(1)求数列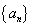
(2) 求证:数列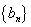
(3) 记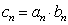
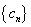
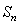
正确答案
见解析。
解析
(1)设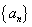
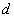
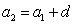
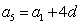
∵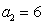
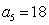
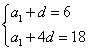
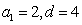
∴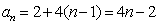
(2)当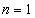
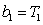
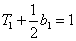
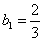
当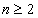
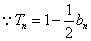
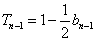
∴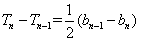
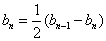
∴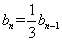
∴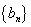
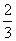
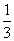
(3)由(2)可知: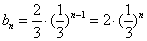
∴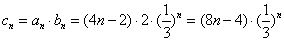
∴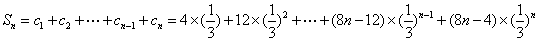
∴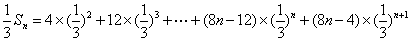
∴
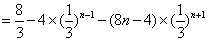
∴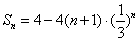
知识点
等差数列







(1)求

(2)记




正确答案
见解析。
解析
(1)由已知可得
解直得,


(2)由(1)得,
由已知得 

①-②得

知识点
已知函数f(x)=

(1)求数列{an}的通项公式an;
(2)令
(3)令cn=


正确答案
见解析。
解析
(1)∵点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴
∴当n=1时,
当n≥2时,an=Sn﹣Sn﹣1=
当n=1时,也适合上式,
因此
(2)由(1)可得:

∴Tn=

两式相减得

∴
(3)证明:由cn=



∴c1+c2+…+cn>2n。
又cn=



∴c1+c2+…+cn=2n+[(








∴2n<c1+c2+…+cn<2n+
知识点
扫码查看完整答案与解析