- 集合与常用逻辑用语
- 共1759题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知抛物线C:y2=4x的焦点为F,过点K(-1,0)的直线l与C相交为A、B两点,点A关于x轴的对称点为D.
(1)证明:点F在直线BD上;
(2)设
正确答案
见解析。
解析
设




(1)将


从而
直线

即
令
所以点

(2)由①知,
因为 
故 
解得
所以
又由①知
故直线BD的斜率
因而直线BD的方程为
知识点
已知






正确答案
解析
考查的是等差数列的基本计算,技术难度并不高,通项公式和前n项和的常规考法。因为 


知识点
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级,若S≤4,则该产品为一等品,现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率。
正确答案
见解析
解析
(1)计算10件产品的综合指标S,如下表:
其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,故该样本的一等品率为
(2)①在该样本的一等品中,随机抽取2件产品的所有可能结果为{A1,A2},{A1,A4},{A1,A5},{A1,A7},{A1,A9},{A2,A4},{A2,A5},{A2,A7},{A2,A9},{A4,A5},{A4,A7},{A4,A9},{A5,A7},{A5,A9},{A7,A9},共15种。
②在该样本的一等品中,综合指标S等于4的产品编号分别为A1,A2,A5,A7,则事件B发生的所有可能结果为{A1,A2},{A1,A5},{A1,A7},{A2,A5},{A2,A7},{A5,A7},共6种,所以P(B)=
知识点
设a,b∈R,则“(a-b)·a2<0”是“a<b”的( )。
正确答案
解析
因为a2≥0,而(a-b)a2<0,所以a-b<0,即a<b;由a<b,a2≥0,得到(a-b)a2≤0可以为0,所以“(a-b)a2<0”是“a<b”的充分而不必要条件。
知识点
对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( A )
正确答案
解析
由概念知中位数是中间两数的平均数,即
知识点
设


①给定向量


②给定向量




③给定单位向量




④给定正数




上述命题中的向量


正确答案
解析
①②容易判断是对的,③给定单位向量









知识点
已知实数x,y满足:
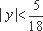
正确答案
略
解析
∵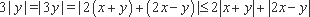
由题设
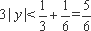
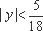
知识点
设集合

正确答案
解析
略
知识点
在等差数列


正确答案
解析
由已知
知识点



正确答案
解析
知识点
过坐标原点


























(1)求
(2)求

(3)设







正确答案
(1)



解析
(1)如图,由






同理

(2)如图,法1:点






消去

又
从而
由①有
②-①得
即

所以


(3)因为
所以数列


因正整数





则




而
因为

又


故

知识点
已知双曲线










(1)求实数
(


(3)若点










正确答案
见解析。
解析
(1)解:设双曲线

由题意可得
解得
(2)证明:由(1)可知,直线



因为

所以
因为点



所以

所以直线


(3)证法1:设点







设

即
整理,得
由①×③,②×④得
将


将⑤代入⑦,得
所以点

证法2:依题意,直线

设直线

由
消去

因为直线



则有
设点


整理得
将②③代入上式得
整理得
因为点


联立④⑤消去

所以点

知识点
已知椭圆


(1)求椭圆
(2)若平行于










正确答案
见解析
解析
(1)设椭圆
将

解得

设点


又




故



(2)因为直线







设


又
故
又
所以上式分子
故
所以直线

知识点
已知命题

正确答案
解析
略
知识点
扫码查看完整答案与解析
































































