- 集合与常用逻辑用语
- 共1759题
3.在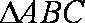
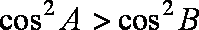
正确答案
解析
因为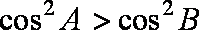

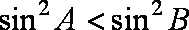
即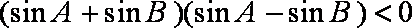
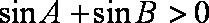
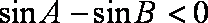
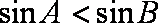
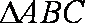
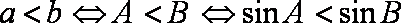
知识点
3.“

正确答案
解析
∵a<-4,f(x)=ax+3,
∴f(0)=3>0,f(1)=a+3<(-4)+3=-1<0,f(0)•f(1)<0
∴函数f(x)=ax+3在区间[0,1]上存在零点x0.
∴a<-4”是“函数f(x)=ax+3在区间[-1,1]上存在零点x0”的充分条件;
反之,若函数f(x)=ax+3在区间[-1,1]上存在零点,则f(-1)•f(1)≤0,即(-a+3)(a+3)≤0解得a≤−3或a≥3,
∴a<-4不是“函数f(x)=ax+3在区间[-1,2]上存在零点的必要条件.故选A.
知识点
8.已知直线l,m,平面α,β且l⊥α,m⊂β,给出四个命题,其中真命题的个数是( )
①若α∥β,则l⊥m;
②若l⊥m,则α∥β;
③若α⊥β,则l∥m;
④若l∥m,则α⊥β.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知命题



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.下面给出四个命题:
①函数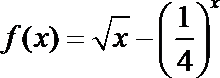
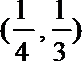
②若函数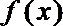
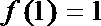
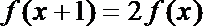
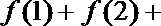
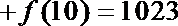
③“若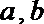
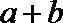
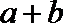
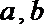
④“若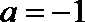
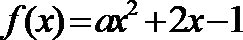
其中所有正确的命题序号是( ).
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
试题分析:方面,“非







知识点
2.设p、q是两个命题,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.条件





正确答案
充分不必要条件
解析
解析已在路上飞奔,马上就到!
知识点
6.给定下列四个命题:
①若两个平面互相垂直,那么分别在这两个平面内的任意两条直线也互相垂直;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③若两个平面平行,则其中一个平面内的直线必平行于另一个平面;
④若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
其中,为真命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.我们称离心率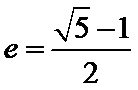
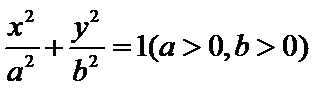
①长半轴长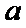
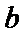
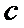
②一个长轴顶点与其不同侧的焦点以及一个短轴顶点构成直角三角形.
③以两条通经的4个端点为顶点的四边形为正方形.
④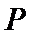
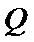
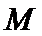
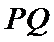
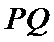
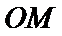
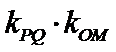
其中正确命题的序号为____________。
正确答案
①②③④
解析
解析已在路上飞奔,马上就到!
知识点
6.“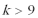
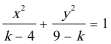
正确答案
解析
方程“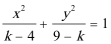
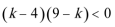
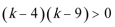
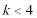
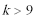
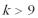
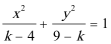
知识点
6.已知下列三组条件:
(1)

(2)


(3)






其中

正确答案
(1)(2)
解析
解析已在路上飞奔,马上就到!
知识点
8.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析







