- 集合与常用逻辑用语
- 共1759题
3.定义运算:
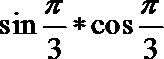
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若a>0,b>0,且函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,则不等式f(x)·g(x)<0的解集是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.条件



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.用反证法证明命题:“已知a,b∈N,若ab不能被7整除,则a与b都不能被7整除”时,假设的内容应为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在下列给出的命题中,
①函数

②对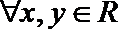

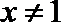
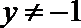
③若实数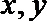



④若

⑤把函数


其中正确结论的序号是__________。
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
6.下列命题中,真命题是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.命题“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知





正确答案
解:若p为真,则
若q为真,则二次函数的对称轴

因为“p且q”为假,“p或q”为真,所以“p真q假”或“p假q真”,
解析
解析已在路上飞奔,马上就到!
知识点
11.设p:|4x-3|≤1,q: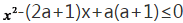
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知两点


①
② 
③ 
④
其中为“和谐直线”的是______________(请写出符合题意的所有编号).
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
17.通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
(1)从这60名男生中按是否看营养说明采取分层抽样的方法,抽取一个容量为6的样本,问样本中看与不看营养说明的男生各有多少名?
(2)从(1)中的6名男生样本中随机选取2名作深度采访,求选到看与不看营养说明的男生各1名的概率;
(3)根据以上列联表,是否有85%的把握认为“性别与在购买食物时看营养说明”有关?
参考公式:

参考值表:
正确答案
解: (1)根据分层抽样可得:样本中看营养说明的男生有

(2)记样本中看营养说明的4名男生为
















其中符合要求的是







故所求的概率为
(3)假设

由题设条件得:
因为由

解析
解析已在路上飞奔,马上就到!
知识点
2.下列命题中,说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若m
②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;
④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析