- 集合与常用逻辑用语
- 共1759题
6.按下图所示的程序框图运算:若输出k=2,则输入x的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对于下列命题:
① 在


② 在




③ 设



④ 将函数


其中正确命题的编号是___________。(写出所有正确结论的编号)
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
15.对于函数
①等式
②函数

③函数
④若
⑤若
其中所有正确结论的序号为________________。
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
3.下列命题中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列四个命题中的真命题为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.“2a>2b”是“lna>lnb”的( )
正确答案
解析
“2a>2b”⇔“a>b”, “lna>lnb”⇔“a>b>0”,∵“a>b”是“a>b>0”的必要不充分条件,故“2a>2b”是“lna>lnb”的必要不充分条件,故选B.
知识点
7.下列4个命题:
①命题“若
②“


③命题“


④已知p,q为简单命题,则“

其中正确的命题个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.下图为某地区2012年1月到2013年1月鲜蔬价格指数的变化情况
记




(Ⅰ) 比较2012年上半年与下半年鲜蔬价格指数月平均值的大小(不要求计算过程);
(Ⅱ) 直接写出从2012年2月到2013年1月的12个月中价格指数环比下降的月份. 若从这12个月中随机选择连续的两个月进行观察,求所选两个月的价格指数均环比下降的概率;
(Ⅲ) 由图判断从哪个月开始连续三个月的价格指数方差最大。 (结论不要求证明)
正确答案
解:(Ⅰ)上半年的鲜疏价格的月平均值大于下半年的鲜疏价格的月平均值.
(Ⅱ)从2012年2月到2013年1月的12个月中价格指数环比下降的月份有4月、5月、6月、9月、10月.
设“所选两个月的价格指数均环比下降”为事件A,
在这12个月份中任取连续两个月共有11种不同的取法,
其中事件A有(4月,5月),(5月,6月),(9月,10月),共3种情况.
(Ⅲ)从2012年11月开始,2012年11月,12月,2013年1月这连续3个月的价格指数方差最大.
解析
解析已在路上飞奔,马上就到!
知识点
15.对于函数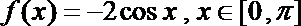
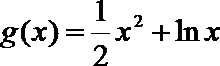
①函数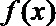
②方程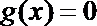
③函数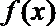
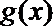
④若函数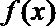
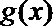
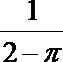
其中正确的是__________(把所有正确命题的序号都填上)
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
5.已知三条不重合的直线m,n,l,两个不重合的平面α,β有下列命题:
①若m∥n,n
②若l⊥α,m⊥β,且l∥m,则α∥β
③若m

④若α⊥β,α

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知⊙


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设



①若

②若l⊥m,则

那么( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.给出下列命题:
①在区间(0,+∞)上,函数y=x-1,
②若logm3<logn3<0,则0<n<m<1;
③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
④若函数f(x)=3x-2x-3,则方程f(x)=0有2个实数根,
其中正确命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出定义:若
①y=f(x)的定义域是R,值域是
②点(k,0)是y=f(x)的图象的对称中心,其中k∈Z;
③函数y=f(x)的最小正周期为1;
④函数y=f(x)在
则上述命题中真命题的序号是__________.
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
3.下列有关命题的叙述,
①若

②“

③命题



④命题“若



其中错误的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

















