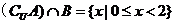- 集合与常用逻辑用语
- 共1759题
已知集合M={x|一3<x<3，x∈Z），N={x|x<1}，则M
A{
B
C{-3，-2，-1，0,1）
D{-2，一1，0）
正确答案
解析
因为集合M={x|一3<x<3，x∈Z}={-2，-1,0,1,2，}，N={x|x<1}，所以M
知识点
1.若集合A={x|x＞0}，B={x|x＜3}，则A∩B等于（ ）
正确答案
解析
根据题意，在数轴上表示出A、B，可得：进而由交集的定义，取两个集合的公共部分，可得A∩B={x|0＜x＜3}，故选B。
知识点
1.设全集为R, 函数
A(－∞,1)
B(1, + ∞)
C
D
正确答案
解析
略。
知识点
已知集合
（1）求
（2）若
正确答案
见解析
解析
解析：（1）
（2）如图，
a>3
知识点
设函数
正确答案
解析
因为
知识点
若
正确答案
解析
知识点
已知全集
A
B
C
D
正确答案
解析
知识点
已知集合
（1）若M={
（2）在（Ⅰ）中的集合M内，随机取出一个元素
正确答案
见解析。
解析
（1）M ={(-2, -1)，(-2, 1)，(0, -1)，(0, 1)，(2, -1)，(2, 1)}.
（2）记“以(x，y)为坐标的点位于区域D内”为事件A.
集合M中共有6个元素，即基本事件总数为6，区域D含有集合M中的元素4个，
所以
故以(x，y)为坐标的点位于区域D内的概率为
知识点
设集合
正确答案
解析
集合
知识点
如图，一空间几何体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC
（1）证明：平面ACD⊥平面ADE；
（2）若AB=2，BC=1，
正确答案
见解析。
解析
（１）证明：∵ DC
∵AB是圆O的直径 ∴
∴
∵四边形DCBE为平行四边形
∴DE//BC
∴
又∵
（2）所求几何体的体积：
∵
∴
∴
∴该几何体的体积
知识点
1.设全集U={a，b，c，d}，集合A={a，b}，B={b，c，d}，则（∁UA）∪（∁UB）=（ ）
正确答案
解析
∵U={a，b，c，d}，集合A={a，b}，B={b，c，d}，
∴（∁UA）∪（∁UB）={c，d}∪{a}={a，c，d}，
故选：D
知识点
1.已知全集
A
B
C
D
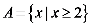
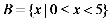
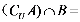
正确答案
解析
由题意易知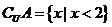
故选C.
知识点
2.已知全集
A
B
C
D
正确答案
解析
由题意得：
知识点
1.集合A={x|y=
正确答案
解析
集合A={x|y=
知识点
12.定义在R上的函数f（x）满足：f（x）+f′（x）＞1，f（0）=4，则不等式exf（x）＞ex+3（其中e为自然对数的底数）的解集为（ ）
正确答案
解析
解：设g（x）=exf（x）﹣ex，（x∈R），
则g′（x）=exf（x）+exf′（x）﹣ex=ex[f（x）+f′（x）﹣1]，
∵f（x）+f′（x）＞1，
∴f（x）+f′（x）﹣1＞0，
∴g′（x）＞0，
∴y=g（x）在定义域上单调递增，
∵exf（x）＞ex+3，
∴g（x）＞3，
又∵g（0）═e0f（0）﹣e0=4﹣1=3，
∴g（x）＞g（0），
∴x＞0
故选：A．
知识点
扫码查看完整答案与解析