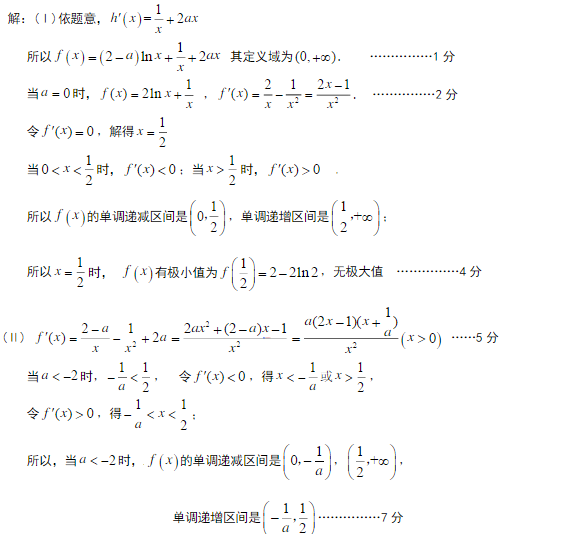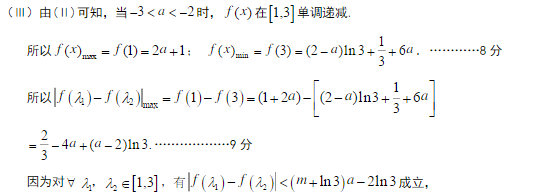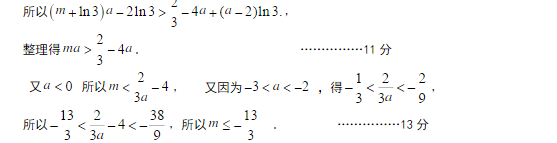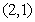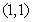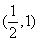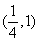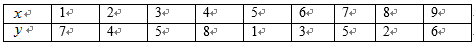- 集合与常用逻辑用语
- 共1759题
已知函数
(1)若


(2)求函数
正确答案
见解析。
解析


(1)若


因为

所以切线方程为

(2)由于

⑴ 当


令


且当



所以



⑵ 当

① 当


得

若




若








② 当

令


若




若





当





所以



综上所述,当




当


当


知识点
已知函数f(x)=
正确答案
(﹣1,1]
解析
①当m≤0时,f(x)=2﹣x﹣1在区间[﹣1,m]上为减函数
故f(m)=2﹣m﹣1<1,
故2﹣m<2=21,解得m>﹣1,
则此时﹣1<m≤0;
②当m>0时,f(x)=2﹣x﹣1在区间[﹣1,0]上为减函数,


解得0<m≤1。
综上可知,则m的取值范围是(﹣1,1]。
知识点
已知函数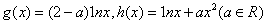
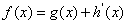
(1)当a=0时,求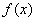
(2)当a<-2时,求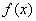
(3)当-3<a<-2时,若存在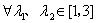
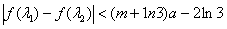
正确答案
见解析。
解析
知识点
执行如图所示的程序框图,输出的结果是
正确答案
解析
略
知识点
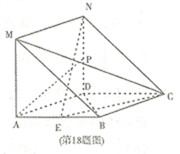
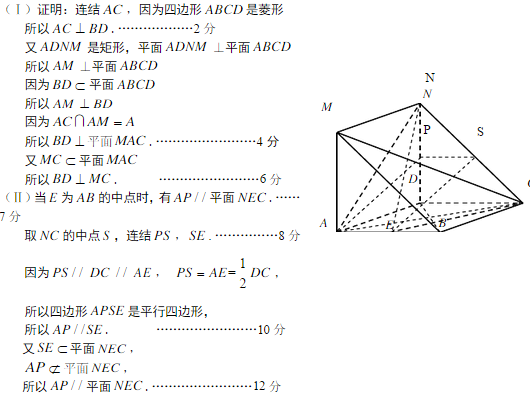
如图
















(1) 求证:

(2) 在线段




(3) 求点

正确答案
见解析。
解析
(1)连结


在

所以
在图

在

又






(2) 当




证明如下:
因为

又





(3) 由(1)知



设点



即


所以



知识点
在区间[1,5]和[2,6]内分别取一个数,记为a 和b,则方程

正确答案
解析
略
知识点
已知向量

(1)求角C的大小;
(2)若
正确答案
见解析。
解析
知识点
在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面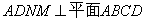
(1)求证: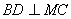
(2)在线段AB上是否存在点E,使得AP//平面NEC,若存在,说明其位置,并加以证明;若不存在,请说明理由.
正确答案
见解析。
解析
知识点
设数列



(1)求数列
(2)在


正确答案
见解析。
解析
知识点
已知点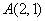
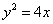
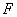
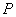
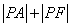
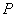
正确答案
解析
略
知识点
已知定义在








正确答案
解析
略
知识点
设集合U={0,l,2,3,4,5,6},M ={l,3,5},N={2,4,6},则(
正确答案
解析
略
知识点
对于函数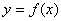
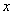
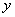
数列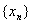
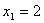
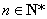
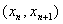
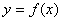
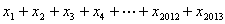
正确答案
解析
略
知识点
函数







正确答案
①②③
解析
略
知识点
为了解高三学生综合素质测评情况,对2000名高三学生的测评结果进行了统计,其中优秀、良好、合格三个等级的男、女学生人数如下表:
(1)若按优秀、良好、合格三个等级分层,在这2000份综合素质测评结果中随机抽取80份进行比较分析,应抽取综合素质测评结果是优秀等级的多少份?
(2)若

正确答案
(1)
(2)
解析
(1)由表可知,优秀等级的学生人数为:

因为
故在优秀等级的学生中应抽取
(2)设“优秀等级的学生中男生人数比女生人数多”为事件
因为




所以数组





其中满足








所以
故优秀等级的学生中男生人数比女生人数多的概率为
知识点
扫码查看完整答案与解析