集合与常用逻辑用语_章节学习

1

题型：单选题

|

单选题 · 5 分

在实数集中，我们定义的大小关系“”为全体实数排了一个“序”，类似的，我们在平面向量集上也可以定义一个称为“序”的关系，记为“”，定义如下：

对于任意两个向量，当且仅当“”或“”，

按上述定义的关系“”，给出如下四个命题：

①若,则；

②若,则；

③若,则对于任意,；

④对于任意向量，,若，则.

其中真命题的序号为（）

A①②④

B①②③

C①③④

D②③④

正确答案

B

解析

（1）①显然正确

（2）设

由,得“”或“”

,则

若“”且“”,则,所以

若“” 且“”,则,所以

综上所述，若,则

所以②正确

（3）设，则

由,得“”或“”

若，则,所以

综上所述，若,则对于任意,

所以③正确

（4）

由得 “”或“”

若“”且“”，则,

所以，所以

所以④不正确，综上所述，①②③正确，选B

知识点

四种命题及真假判断

1

题型：简答题

|

简答题 · 12 分

已知命题：方程在［-1，1］上有解；命题：只有一个实数满足不等式，若命题“或”是假命题，求的取值范围。

正确答案

见解析。

解析

由题意.

若正确，的解为或 …………2分

若方程在［-1，1］上有解，

只需满足-1 ……………………………4分

即 ……………………………6分

若正确，即只有一个实数满足，

则有即或2 ……………………8分

若或是假命题，则和都是命题， ………………………………10分

有所以a的取值范围是（1，0）（0，1） …………12分

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

命题“∀x∈R，x2+1≥1”的否定是（　　）

A∀x∈R，x2+1＜1

B∃x∈R，x2+1≤1

C∃x∈R，x2+1＜1

D∃x∈R，x2+1≥1

正确答案

C

解析

解：∵原命题“∀x∈R，有x2+1≥1”

∴命题“∀x∈R，有x2+1≥1”的否定是：

∃x∈R，使x2+1＜1。

故选C。

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

在中，向量满足，下列说法正确的是 ①；②；③存在非零实数使得

A①②

B①③

C②③

D①②③

正确答案

C

解析

由题意知为等腰三角形,由知为边的中点,故成立; 故成立，直线AP为的角平分线,表示的角平分线方向上的向量,故与共线。

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

“”是“函数在区间内单调递增”的………（）

A充分非必要条件

B必要非充分条件

C充要条件

D既非充分又非必要条件

正确答案

A

解析

略

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

气象台预报“茂名市明天降雨的概率是80%”，下列理解正确的是（　　）

A茂名市明天将有80%的地区降雨

B茂名市明天将有80%的时间降雨

C明天出行不带雨具肯定要淋雨

D明天出行不带雨具淋雨的可能性很大

正确答案

D

解析

茂名市明天降雨的概率是80%的含义是：茂名市明天降雨的可能性达80%，∴D正确。

故选D

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

“a=﹣1”是“直线a2x﹣y+6=0与直线4x﹣（a﹣3）y+9=0互相垂直”的（　　）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

A

解析

当a=﹣1时，直线分别为x﹣y+6=0与4x+4y+9=0，则两直线垂直；

当直线a2x﹣y+6=0与4x﹣（a﹣3）y+9=0互相垂直时，则有4a2+（a﹣3）=0，解析得a=﹣1或，

故选A。

知识点

四种命题及真假判断

1

题型：简答题

|

简答题 · 12 分

命题P：关于x的不等式，对一切恒成立，命题q：函数是增函数，若为真，为假，求实数a的取值范围。

正确答案

见解析。

解析

……2分，

………………2分

为真，为假，一真一假，…1分

p真q假时，，…………2分

……1分假真，，……2分

……1分 ……1分

知识点

四种命题及真假判断

1

题型：简答题

|

简答题 · 12 分

已知命题：方程有两个不等的负根，命题：无实根，且为真命题，求实数的取值范围。

正确答案

见解析。

解析

由已知可知，，解得，

，解得 …….6分

且为真，同时为真，则， …….9分

，实数的取值范围是. …….12分

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

下列命题中的真命题是

A

B＞

C＜

D＞

正确答案

B

解析

＞3，，所以A、C、D都是假命题.令，得对于恒成立，故上是增函数，所以＞＞，故B是真命题.

知识点

四种命题及真假判断

1

题型：简答题

|

简答题 · 12 分

已知：，：（），若“非”是“非”的必要而不充分条件，求实数的取值范围。

正确答案

见解析。

解析

由：，解得，

∴“非”：。

由：

解得

∴“非”：

由“非”是“非”的必要而不充分条件可知：。

解得。

∴满足条件的m的取值范围为。

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

下列各命题中正确的命题是

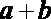
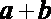
① “若a, b都是奇数，则是偶数”的逆否命题是“若不是偶数，则a, b都不是奇数”；

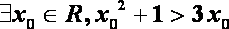
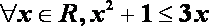
② 命题“”的否定是“” ；

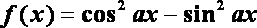
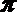
③ “函数的最小正周期为” 是“a=1”的必要不充分条件；

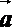
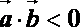
④“平面向量与的夹角是钝角”的充分必要条件是“” 。

A②③

B①②③

C①②④

D③④

正确答案

A

解析

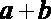
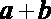
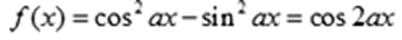
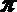
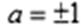
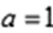
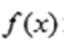
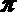
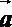
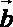
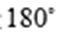
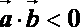
若a, b都是奇数，则是偶数的逆否命题是是偶数，则a, b都是奇数，所以①不对；②对；，若最小正周期为，则，反之当，函数最小正周期为，则③对；当向量与的夹角是是，也有，则④错

知识点

四种命题及真假判断

1

题型：填空题

|

填空题 · 5 分

已知函数则

（1）______________;

（2）下列三个命题中，所有真命题的序号是__________.

①函数是偶函数；

②任取一个不为零的有理数,对任意的恒成立；

③存在三个点，使得为等边三角形。

正确答案

（1）1

（2）①②③

解析

（1）依题意可知，当时，；当时，.因此.

（2）对于①，当时，，此时；当时，，此时，因此对任意的，都有，所以函数是偶函数，①正确.对于②，任取一个不为零的有理数，当时，,；当时，，因此对任意的，都有，②正确.对于③，取点，易知点均在函数的图象上，且是等边三角形，③正确.综上所述，所有真命题的序号是①②③。

知识点

四种命题及真假判断

1

题型：填空题

|

填空题 · 5 分

现有如下命题：

①过平面外一点有且只有一条直线与该平面垂直；

②过平面外一点有且只有一条直线与该平面平行；

③如果两个平行平面和第三个平面相交，那么所得的两条交线平行；

④如果两个平面相互垂直，那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内。

则所有真命题的序号是　

正确答案

①③④　

解析

①过平面外一点有且只有一条直线与该平面垂直，正确；

②过平面外一点有且只有一条直线与该平面平行，错误，应该是有无数条直线与该平面平行；

③如果两个平行平面和第三个平面相交，那么所得的两条交线平行，正确，由平面与平面平行的性质定理可得；

④如果两个平面相互垂直，那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内，正确，

由平面与平面垂直的性质定理可得。

故答案为：①③④

知识点

四种命题及真假判断

1

题型：单选题

|

单选题 · 5 分

下列四个命题中真命题的个数是（）

①“”是“”的充分不必要条件；

②命题“”的否定是“”；

③“若，则”的逆命题为真；

④命题，命题，则为真。

A0

B1

C2

D3

正确答案

D

解析

命题①中，是不等式的解集的真子集，“”是“”的充分不必要条件，①正确.命题②显然正确.命题③中，当时，其逆命题不成立，故③错.命题④中，为真，为假，所以为真，故④正确.综上所述，真命题的个数为3.故选.

知识点

四种命题及真假判断

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点