- 带电粒子在混合场中的运动
- 共247题
如图所示,在两水平极板间存在匀强电场和匀强磁场,电场方向竖直向下,磁场方向垂直于纸面向里,一带是粒子以某一速度沿水平直线通过两极板,若不计重力,下列四个物理量中哪一个改变时,粒子运动轨迹不会改变( )
正确答案
解析
粒子能水平通过电容器则qE=qvB,则改变电荷量不会打破平衡使粒子的运动轨迹发生改变。
知识点
如图所示,二块水平放置.相距为d的长金属板接在电压可调的电源上。两板之间的右侧区域存在方向垂直纸面向里的匀强磁场。将喷墨打印机的喷口靠近上板下表面,从喷口连续不断喷出质量均为m.水平速度均为v0.带相等电荷量的墨滴。调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动,进入电场.磁场共存区域后,最终垂直打在下板的M点。
(1)判断墨滴所带电荷的种类,并求其电荷量;
(2)求磁感应强度B的值;
(3)现保持喷口方向不变,使其竖直下移到两板中间位置。为了使墨滴仍能到达下板M点应将磁感应强度调至B',则B'的大小为多少?
正确答案
见解析。
解析
(1) 墨滴在电场区域做匀速直线运动,有
得
由于电场方向向下,电荷所受电场力向上,可知:
墨滴带负电荷。
(2) 进入电场.磁场共存区域后,重力与电场力平衡,磁场力做匀速圆周运动的向心力,
考虑墨滴进入磁场和挡板的几何关系,可知墨滴在该区域恰完成四分之一圆周运动,则半径R=d,由此可得:
(3)根据题设,墨滴运动轨迹如图,设圆周运动半径为
由图示可得:
得:
知识点
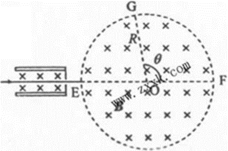
如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔










(1)求粒子到达


(3)若已保证了粒子未与极板相撞,为使粒子在

正确答案
见解析。
解析
(1)粒子由


由①式得

设粒子的加速度大小为

由运动学公式得

联立③④式得

(2)设磁感应强度大小为B,粒子在磁场中做匀速圆周运动的半径为R,由牛顿第二定律得

要使粒子在磁场中运动时不与极板相撞,须满足

联立②⑥⑦式得

(3)设粒子在两边界之间无场区向左匀速运动的过程用时为

联立②⑤⑨式得

若粒子再次达到


联立91011式得

设粒子在磁场中运动的时间为

联立⑩⑿⒀式得

设粒子在匀强磁场中做匀速圆周运动的周期为T,由6式结合运动学公式得

由题意得

联立⒁⒂⒃式得

知识点
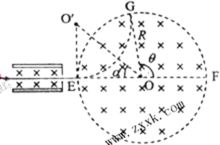
如图,与水平面成45°角的平面MN将空间分成I和II两个区域。一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平向右射入I区。粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里。求粒子首次从II区离开时到出发点P0的距离。粒子的重力可以忽略。
正确答案
带电粒子进入电场后,在电场力的作用下沿抛物线运动,其加速度方向竖直向下,设其大小为a,由牛顿定律得qE=ma①
设经过时间t0,粒子从平面MN上的点P1进入磁场,由运动学公式和几何关系得
v0t0=at02②
粒子速度大小V1为 V1=
设速度方向与竖直方向的夹角为α,则 tanα=
此时粒子到出发点P0的距离为 s0=
此后,粒子进入磁场,在洛仑兹力作用下做匀速圆周运动,圆周半径为 r1=
设粒子首次离开磁场的点为P2,弧P1P2所张的圆心角为2β,则P1到点P2的距离为
s1=2r1sinβ⑦
由几何关系得 α+β=45°⑧
联立①②③④⑤⑥⑦⑧式得 s1=
点P2与点P0相距 l=s0+s1⑩
联立①②⑤⑨⑩解得 l=
解析
略。
知识点
右图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁感应强度大小为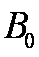
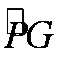
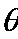
(1)离子速度的大小;
(2)离子的质量。
正确答案
见解析
解析
由题设知,离子在平行金属板之间做匀速直线运动,安所受到的向上的压力和向下的电场力平衡
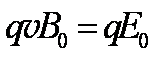
式中,
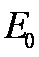
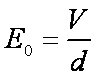
由①②式得 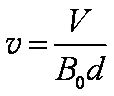
(2)在圆形磁场区域,离子做匀速圆周运动,由洛伦兹力公式和牛顿第二定律有
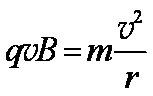
式中,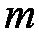
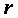
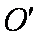
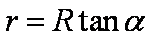
式中,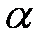
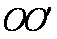
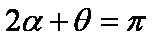
联立③④⑤⑥式得,离子的质量为 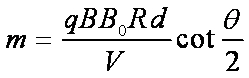
知识点
扫码查看完整答案与解析