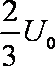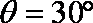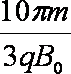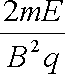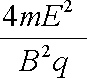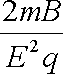- 带电粒子在混合场中的运动
- 共247题
如图所示,在电子枪右侧依次存在加速电场,两水平放置的平行金属板和竖直放置的荧光屏。加速电场的电压为U1。两平行金属板的板长、板间距离均为d。荧光屏距两平行金属板右侧距离也为d。电子枪发射的质量为m、电荷量为–e的电子,从两平行金属板的中央穿过,打在荧光屏的中点O。不计电子在进入加速电场前的速度及电子重力。
(1)求电子进入两金属板间时的速度大小v0;
(2)若两金属板间只存在方向垂直纸面向外的匀强磁场,求电子到达荧光屏的位置与O点距离的最大值
(3)若两金属板间只存在竖直方向的匀强电场,两板间的偏转电压为U2,电子会打在荧光屏上某点,该点距O点距离为
正确答案
见解析。
解析
(1)设电子经电场加速后进入偏转场区的速度大小为v0,由动能定理得


(2)偏转场区中只有匀强磁场时,电子进入磁场区受洛仑兹力作用做匀速圆周运动,经磁场偏转后,沿直线运动到荧光屏。磁场的磁感应强度越大,偏转越大,电子偏转的临界状态是恰好从上板的右端射出,做直线运动到达荧光屏。它的位置与O点距离即为最大值
电子做圆周运动,有
由图可得 

可得 

由③式和
得 
(3)偏转区内只有匀强电场时,电子进入偏转区做匀加速曲线运动,如图所示。
离开偏转电场时沿电场方向的位移
速度方向偏转角设为
打到荧光屏的位置距O点的距离
可得
由
方案一:保持U1的大小不变,将偏转电压U2加倍即可。
方案二:保持U2的大小不变,将加速电压U1减半即可。
知识点
某放置在真空中的装置如图甲所示,水平放置的平行金属板A、B中间开有小孔,小孔的连线与竖直放置的平行金属板C、D的中心线重合。在C、D的下方有如图所示的、范围足够大的匀强磁场,磁场的理想上边界与金属板C、D下端重合,其磁感应强度随时间变化的图象如图乙所示,图乙中的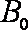
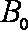
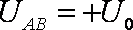

(1)求金属板C、D之间的电势差UCD。
(2)求粒子离开偏转电场时速度的大小和方向。
(3)规定垂直纸面向里的磁场方向为正方向,在图乙中t=0时刻该粒子进入磁场,并在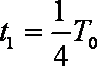
正确答案
(1)
(2)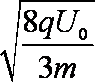
(3)
解析
(l)设粒子在加速电场中被加速后获得的速度为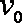
由动能定理得:
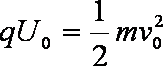
解得: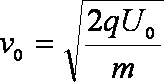
设粒子在偏转电场中运动的加速度为a,运动时间为t ,由牛顿运动定律和类平抛运动规律可得:
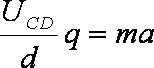


联立解得: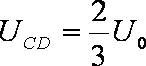
(2)设粒子离开偏转电场时的速度大小为
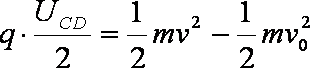
解得: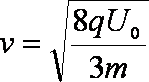
设粒子由k点离开电场时偏转角为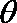

解得: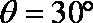
(3)由作图和分析可得,粒子在磁场中的运动轨迹如下图所示。
粒子在磁场中做圆周运动的周期为: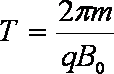
粒子从k进入磁场,沿逆时针方向运动,由“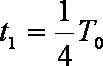

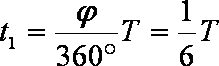
故有:
联立上述各式解得: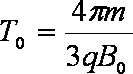
结合图乙可知,粒子经过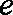

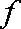

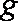

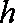



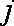
则该粒子从射入磁场到离开磁场的总时间为:
t总=
即:t总=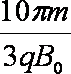
知识点
如图甲所示,两块相同的平行金属板M、N正对着放置,相距为









⑴若M、N间的电势差

⑵若M、N间接入如图乙所示的随时间t变化的电压

⑶在上述⑵问的情形下,当M、N间的电压不同时,质子从S1处到打在收集屏PQ上经历的时间t会不同,求t的最大值.
正确答案
见解析
解析
(1)根据动能定理
有 
(2)质子在板间运动,根据动能定理, 有
质子在磁场中运动,根据牛顿第二定律,有
若质子能打在收集屏上,轨道半径
半径
解得板间电压
结合图象可知:质子在


(3)M、N间的电压越小,质子穿出电场进入磁场时的速度越小,质子在极板间经历的时间越长,同时在磁场中运动轨迹的半径越小,在磁场中运动的时间也会越长,出磁场后打到收集屏前作匀速运动的时间也越长,所以当质子打在收集屏的P端时,对应时间t
最长,两板间的电压此时为
在板间电场中运动时间
在磁场中运动时间
出磁场后打到收集屏前作匀速运动的时间
所以,运动总时间
或t
知识点
如图所示,在平面直角坐标系xOy的第二象限内有场强大小为E、沿x轴正方向的匀强电场,在第一象限内有一圆形匀强磁场区域(图中未画出),磁场方向垂直xOy平面,圆形匀强磁场区域的边界与x轴相切于点P(2L,0)。两个质子(质子质量m,电荷量q,不计重力)a、b以相等的速率沿不同方向从P点同时射入磁场区,其中a的速度方向沿y轴正方向,b的速度方向与x轴正方向的夹角
(1)求磁感应强度B的大小和质子在磁场中运动速度v的大小;
(2)求质子在电场中运动离y轴的最远距离x;
(3)两个质子离开电场后会先后经过同一点M,求质子b从开始运动到经过M点的时间t;
(4)若只将第二象限内的匀强电场方向变为沿y轴负方向,仍使a、b以原来的速度射入磁场区,求a、b经过x轴上的两点间的距离
正确答案
(1)v=
(2)
(3)t=3t0+

(4)Δx=
解析
(1)两质子的运动轨迹如图,在磁场中的运动周期为:

a在磁场中转过90°圆心角,时间
b在磁场中转过150°圆心角,时间
则:t0= tb-ta =
解得:
由a的轨迹可知质子在磁场的运动半径:R= L
由
得:
(2)质子在电场中,由动能定理得:
-qEx=-
得:
(3)两质子离开电场后再次返回磁场的轨迹如图,由运动的对称性可知, a、b在磁场中运动时间都是:t1=
b在非场区运动时间:
在电场中:
b在电场中运动时间:

t= t1+t2+t3=3t0+

(4)ha=L,hb=R+Rcos30°=
由

得a、b打在x轴上的两点间的距离:
Δx= xb-xa= v(tb-ta)=
知识点
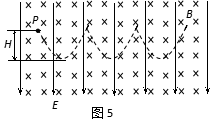
如图5所示,空间存在足够大、正交的匀强电、磁场,电场强度为E、方向竖直向下,磁感应强度为B、方向垂直纸面向里。从电、磁场中某点P由静止释放一个质量为m、带电量为+q的粒子(粒子受到的重力忽略不计),其运动轨迹如图5虚线所示。对于带电粒子在电、磁场中下落的最大高度H,下面给出了四个表达式,用你已有的知识计算可能会有困难,但你可以用学过的知识对下面的四个选项做出判断。你认为正确的是( )
正确答案
解析
略
知识点
扫码查看完整答案与解析