平面向量的基本定理及其意义
共52题

· 平面向量的基本定理及其意义

平面向量的基本定理及其意义
共52题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

P是所在平面内一点，若，其中，则P点一定在（）

A内部

BAC边所在直线上

CAB边所在直线上

DBC边所在直线上

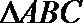
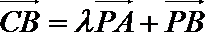
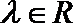
正确答案

解析

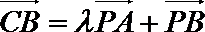
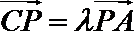
由已知，得，可得，由共线可知，P点一定在AC边所在直线上。

考查方向

本题主要考查了向量的基本运算以及平面几何的综合应用

易错点

向量基本运算需要仔细运算

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：单选题

单选题 · 5 分

4. 在中，，．若点满足，则（）

正确答案

解析

由得，，从而，

所以，故选C。

考查方向

本题考查了向量的线性运算及三角形法则等知识。

解题思路

由出发，进行变换，推出向量

易错点

向量的三角形法则不能熟练掌握，导致运算错误。

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：填空题

填空题 · 5 分

16.在平面直角坐标系中，设是圆:上不同三点，若存在正实数，使得，则的取值范围为 .

正确答案

解析

因为是圆:上不同三点，所以两边平方，得即，又，从而可得，

，

即是

画出可行域如图

又因为，

上式可看成是点（a,b）与点(0,-1)距离的平方和加上点（a,b）与点(0,-1)连线的斜率再减掉1，由图可知，在点（1，0）处它们同时取得最小值，代入可得最小值为2，即取值范围为。

考查方向

本题是解析几何，向量，线性规划的高难度综合题，属于难题。

解题思路

（1）作出点(a,b)的可行域。

（2）找出式子的几何意义。

易错点

（1）易忽视“点是圆:上不同三点”这一条件。

（2）对向量不会处理。

（3）对不会变形。

知识点

平面向量的基本定理及其意义直线与圆的位置关系

题型：单选题

单选题 · 5 分

3．如图，正方形中，为的中点，若，则的值为（）

正确答案

解析

,所以，，选D。

考查方向

本题主要考察了平面向量的基本定理，属于中档题，是高考的热点，解决此类题的关键是会利用平面向量的基本定理，用两个不共线的向量表示平面内任一向量。

易错点

本题易在向量的表示过程中出现错误。

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：简答题

简答题 · 5 分

16．已知点A（0，－1），B（3，0），C（1，2），平面区域P是由所有满足＝λ＋μ（2＜λ≤m，2＜μ≤n）的点M组成的区域，若区域P的面积为16，则m＋n的最小值为_____________．

正确答案

解析

由题可知，设M（x,y），则=（x,y+1）, =（3,1）, =（1,3）,代入条件得

8<x≤3m+n,7<y≤m+3n-1，画出平面区域，利用面积公式可得（m+n）min=

考查方向

本题主要考查线性规划及向量的线性运算。

解题思路

1、画出平面区域

2、化简公式求解．

易错点

本题必须注意利用图像完成。

知识点

平面向量的基本定理及其意义利用基本不等式求最值

继续学习学习下一知识点

下一知识点 : 平面向量的坐标运算

百度题库 > 高考 > 理科数学 > 平面向量的基本定理及其意义

扫码查看完整答案与解析