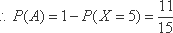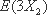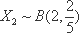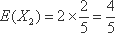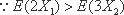- 离散型随机变量及其分布列、均值与方差
- 共180题
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
① 每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为



(1)求甲同学能进入下一轮的概率;
(2)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
正确答案
见解析。
解析
设A、B、C、D分别为第一、二、三、四个问题,用






所以 
(1)记“甲同学能进入下一轮”为事件
则 
由于每题答题结果相互独立,因此


(2)由题意,随机变量
由于每题答题结果相互独立,
所以,
因此 随机变量
所以
知识点
在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手,各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名,观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手。
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和,求X的分布列及数学期望。
正确答案
(1) 
解析
(1)设A表示事件“观众甲选中3号歌手”,B表示事件“观众乙选中3号歌手”,
则P(A)=

∵事件A与B相互独立,
∴观众甲选中3号歌手且观众乙未选中3号歌手的概率为P(A


(2)设C表示事件“观众丙选中3号歌手”,则P(C)=
∵X可能的取值为0,1,2,3,且取这些值的概率分别为
P(X=0)=
P(X=1)=
=
P(X=2)=P(AB



P(X=3)=P(ABC)=
∴X的分布列为
∴X的数学期望
知识点
某联欢晚会举行抽奖活动,举办方设置了甲,乙两种抽奖方案,方案甲的中奖率为

(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为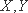

(2)若小明,小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
正确答案
见解析
解析
(1)由已知得:小明中奖的概率为

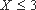
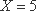
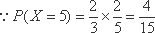

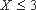
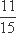
(2)设小明,小红都选择方案甲抽奖中奖的次数为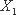
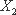
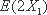
由已知: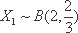
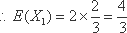
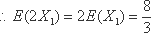

知识点
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元,根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示,经销商为下一个销售季度购进了130 t该农产品,以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润。
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望。
正确答案
(1) 
解析
(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000,
当X∈[130,150]时,T=500×130=65 000.
所以
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
(3)依题意可得T的分布列为
所以ET=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59 400
知识点
已知甲盒中仅有1个球且为红球,乙盒中有m个红球和n个篮球

(a)放入

(b)放入

则 ( )
正确答案
解析


∴


故
又∵
∴
又
∴
=



所以
知识点
扫码查看完整答案与解析