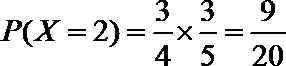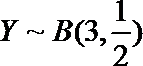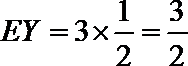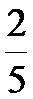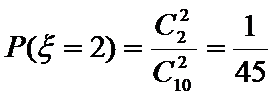- 离散型随机变量及其分布列、均值与方差
- 共180题
19.乒乓球台面被球网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其他情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为,在D上的概率为;对落点在B上的来球,小明回球的落点在C上的概率为,在D上的概率为.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响.求:
(1)小明两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.某品牌汽车的4S店,对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
(1)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位彩用分3期付款”的概率P(A);
(2)4S店销售一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.用


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
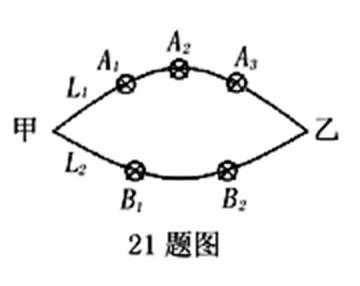
18.如图所示,张先生开车从甲地到乙地有
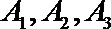

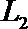
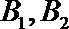
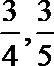
(Ⅰ)若走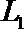
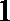
(Ⅱ)若走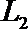
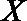
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
正确答案
解:
(Ⅰ)设走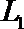
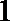
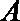
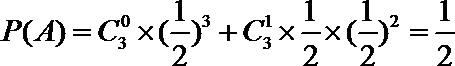
(Ⅱ)依题意,
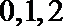
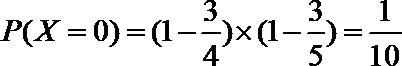
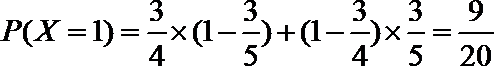
所以随机变量
所以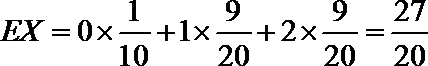
(Ⅲ)设选择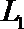
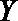
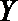
所以
因为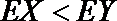
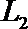

解析
解析已在路上飞奔,马上就到!
知识点
17.某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
(1)补全频率分布直方图(需写出计算过程);
(2)现从[40,55)岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组(每组3人)参加户外体验活动,记A组中年龄在[40,45)岁的人数为


正确答案
(1)0.06;
(2)
解析
本题属于概率统计中的基本问题,题目的难度是逐渐由易到难
(1)因为第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3所以高为0.3/5=0.06。频率直方图如下:
(2)因为[40,45)组、[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,所以三组中应抽出的人数分别为3、2、1.




考查方向
本题考查了概率统计中的频率分布直方图和离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
无
易错点
1、第一问中的高为频率/组距。
2、第二问中随机变量的取值集对应的概率。
知识点
12.赌博有陷阱.某种赌博每局的规则是:赌客先在标记有








正确答案
解析
赌金的分布列为
所以
奖金的分布列为
所以
知识点
18.2016年1月1日起全国统一实施全面两孩政策。为了解适龄民众对放开生育二胎政策的态度,某市选取70后和80后作为调查对象,随机调查了100位,得到数据如下表:
(Ⅰ)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中随机抽取3位,记其中生二胎的人数为

(Ⅱ)根据调查数据,是否有90%以上的把握认为“生二胎与年龄有关”,并说明理由.
参考数据:
(参考公式:

正确答案
(Ⅰ)

(Ⅱ) 90%
解析
试题分析:本题是概率与统计中的基本问题,难度不大,只要正确掌握公式,计算细心,就能正确得出答案。
考查方向
本题主要考查随机变量、二项分布、数学期望等知识,考查运用数学知识解决实际问题的能力和建模能力,难度中等。
解题思路
本题主要考查随机变量、二项分布、数学期望等知识,
解题步骤如下:
利用二项分布的性质,写出分布列和数学期望;
利用题目中给出的参考公式计算、判断,从而得出结果。
易错点
第一问不能正确转化为二项分布列进行求解;
第二问看不懂题中给出的参考公式的意义,因而判断错误。
知识点
18. 现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为

(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分

正确答案
见解析
解析
(Ⅰ)记“该射手恰好命中一次”为事件



由题意知,

由于
(Ⅱ)根据题意,

根据事件的独立性和互斥性得



故
所以
考查方向
解题思路
第一问将所有可能的情况列举出求解,第二问根据随机变量分布列的概念及特征,一次写出当随机变量取不同值得情况
易错点
列举情况不全面
知识点
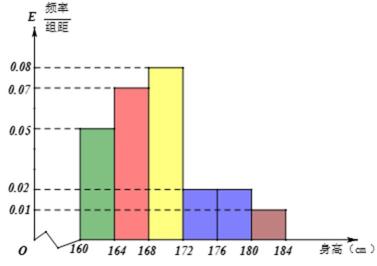
18.某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172 cm以上(含172 cm)的人数;
(Ⅲ)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为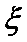
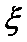
参考数据:若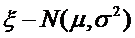
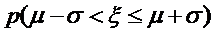
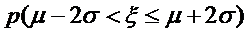
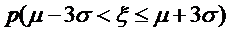
正确答案
(Ⅰ)平均值168.72,高于全市平均值
(Ⅱ)10人.
(Ⅲ)
解析
(Ⅰ)由直方图,经过计算该校高三年级男生平均身高为
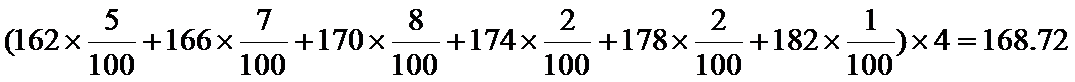
高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168).
(Ⅱ)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×50=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(Ⅲ)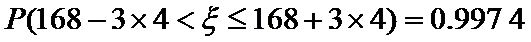
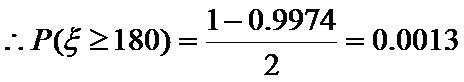
所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量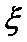
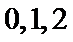
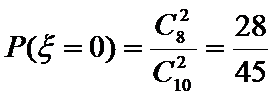
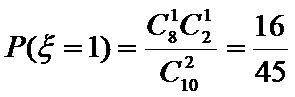
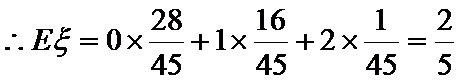
考查方向
解题思路
第一问估算,直接用每组的平均值乘以频率,然后相加即得
第二问先计算后三组的频率和,然后乘以总人数即得
第三问先根据正态分布概率计算出全市前130名是在那个身高区间,然后再计算50个人中有几个在这个区间,最后根据组合数计算出各变量的期望值,再相加即得。
易错点
1、对频率分布直方图认识不清,误把纵坐标当概率
2、对正态分布的意义理解不正确,不能正确计算概率
知识点
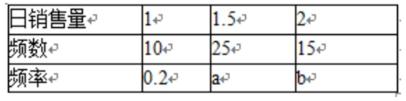
18.某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的结果如下:
(Ⅰ)求表中a,b的值
(Ⅱ)若以上表频率作为概率,且每天的销售量相互独立,
①求5天中该种商品恰有2天销售量为1.5吨的概率;
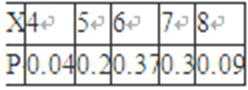
②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和(单位:千元),求X的分布列和期望.
正确答案
(Ⅰ)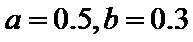
(Ⅱ)①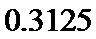
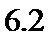
解析
(Ⅰ)∵
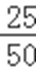
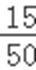
(Ⅱ)①依题意,随机选取一天,销售量为1.5吨的概率p=0.5
设5天中该种商品有X天的销售量为1.5吨,则X~B(5,0.5)
P(X=2)=C52×0.52×(1﹣0.5)3=0.3125 ②X的可能取值为4,5,6,7,8,则
p(X=4)=0.22=0.04 p(X=5)═2×0.2×0.5=0.2 p(X=6)═0.52+2×0.2×0.3=0.37
p(X=7)═2×0.3×0.5=0.3 p(X=8)=0.32=0.09
所有X的分布列为:
EX=4×0.04+5×0.2+6×0.37+7×0.3+8×0.09=6.2.
考查方向
解题思路
本题考查的是频率分布表,

(Ⅰ)由于频率等于频数除以样本容量,所以可根据第二三组的频率求得a,b.
(Ⅱ)利用二项分布的概率公式求出5天中该种商品恰有2天的销售量为1.5吨的概率,求出X的可能取值为4,5,6,7,8,写出分布列,算出期望。
易错点
本题易在分析分布的时候出现错误,也可能在写离散型随机变量的时候出现错误。
知识点
16.已知某种动物服用某种药物一次后当天出现A症状的概率为
(Ⅰ)如果出现A症状即停止试验”,求试验至多持续一个用药周期的概率;
(Ⅱ)如果在一个用药周期内出现3次或4次A症状,则这个用药周期结束后终止试验,试验至多持续两个周期. 设药物试验持续的用药周期数为

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)设持续


所以
则
法二:设用药持续最多一个周期为事件

所以
所以
(Ⅱ)随机变量

所以

所以
考查方向
本题主要考察了概率统计,期望的问题,属于中档题,是高考的热点,解决此类题的关键:会用公式算概率和期望。
易错点
1、本题易在读题时因读不懂题意,导致概率无法计算。
2、因期望中随机变量对应的概率算错而导致出错。
知识点
扫码查看完整答案与解析