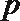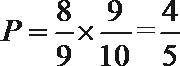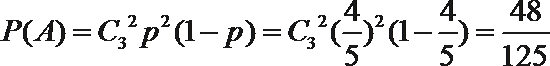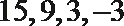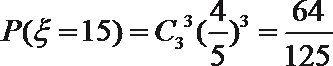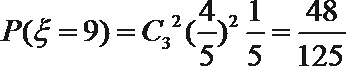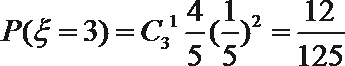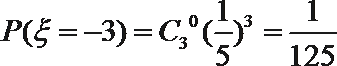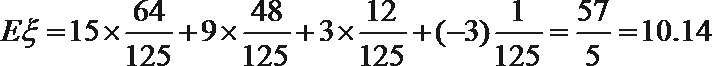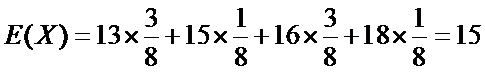- 离散型随机变量及其分布列、均值与方差
- 共180题
17.某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随
机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
(1)补全频率分布直方图(需写出计算过程);
(2)现从[40,55)岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组(每组3人)参加户外体验活动,记A组中年龄在[40,45)岁的人数为
求随机变量

正确答案
(1)0.06;
(2)
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
(1)因为第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3
所以高为0.3/5=0.06。频率直方图如下:
(2) 因为[40,45)组、[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,
所以三组中应抽出的人数分别为3、2、1.






考查方向
本题考查了概率统计中的频率分布直方图和离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
本题考查概率统计,解题步骤如下:
(1)利用直方图的性质求小矩形的高,并补充直方图。
(2)写出随机变量的取值,并求出相应的概率和数学期望。
易错点
(1)第一问中的高为频率/组距。
(2)第二问中随机变量的取值及对应的概率。
知识点
19.(1)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣 小组中按分层抽样的方法抽取50名同学(男

(1)能否据此判断有97.5% 的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5 — 7分钟,乙每次解答一道几何题所用的时间在6 - 8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率,
(3)现从选择做几何题的8名女生中
正确答案
(1)有97.5%的把握认为视觉和空间能力与性别有关;
(2)
(3)
解析
(1)由表中数据得K2的观测值
(2)设甲、乙解答一道几何题的时间分别为x、y分钟,则基本事件满足的区域为
设事件A为“乙比甲先做完此道题”则满足的区域为x>y,
∴由几何概型

(3)由题可知在选择做几何题的8名女生中任意抽取两人,抽取方法有






∴
考查方向
本题考查了独立性检验的应用;离散型随机变量的期望与方差.
解题思路
(1)根据所给的列联表得到求观测值所用的数据,把数据代入观测值公式中,做出观测值,同所给的临界值表进行比较,得到所求的值所处的位置,得到结论;
(2)利用面积比,求出乙比甲先解答完的概率;
(3)确定X的可能值有0,1,2.依次求出相应的概率求分布列,再求期望即可.
易错点
1、第一问中独立性检验知识不熟,公式不会应用;
2、第二问中几何概型转化成面积比
知识点
19.计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量
(Ⅰ)求在未来4年中,至多1年的年入流量超过120的概率;
(Ⅱ)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
若某台发电机运行,则该台发电机年利润为5000万元;若某台发电机未运行,则该台发电机年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
正确答案
(Ⅰ)
(Ⅱ)2
解析
(I)依题意


由二项分布,在未来4年中至多有1年入流量超过120的概率为:

(Ⅱ)记水电站年总利润为
由于水库年入流量总大于40,所以至少安装1台.
①安装1台发电机的情形:
由于水库年入流量总大于40,所以一台发电机运行的概率为1,
对应的年利润

②安装2台发电机的情形:
当

因此
当

因此
所以
所以
③安装3台发电机的情形:
当

因此
当

此时
当

因此
所以
所以
综上,欲使水电站年总利润的均值达到最大,应安装2台发电机.
考查方向
解题思路
(Ⅰ)先求出年入流量X的概率,根据二项分布,求出未来4年中,至少有1年的年入流量超过120的概率;
(Ⅱ)分三种情况进行讨论,分别求出一台,两台,三台的数学期望,比较即可得到.
易错点
第一问较简单,明确二项分布原理就不易出错,第二问分类出错
知识点
18.某单位考勤制度为早中晚刷脸3次,在规定时间内刷脸3次标记为绿色,刷脸2次标记为蓝色,刷脸1次标记为橙色,刷脸0次标记为红色,若标记为橙色,蓝色,红色需要填写申辩说明理由,现有前一天的考勤记录报表显示为甲办公室共计4人,其中标记红色1人,绿色2人,蓝色1人.乙办公室共计3人,其中标记橙色1人,绿色2人.现从甲乙两个办公室各任意抽取2人.
(1)求抽取的4人标记均为绿色的概率;
(2)若标记为红色,蓝色,橙色的人需要提交申辩,设所抽取的4人需要填写申辩的人数为

正确答案
(1)
(2)分布列为
期望为
解析
本题属于古典概型的常见题型,题目的难度是比较稳定,属于中档偏易题,
(1)直接计算出基本事件总数及符合所求的基本事件数;
(2)分析
(3)列出分布列,求出期望。
(1)设“抽取的4人标记均为绿色”为事件

(2) 





易错点
审题不清和考虑不全面导致出错。
知识点
18.某中药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为20万元;有雨时收益为10万元.额外聘请工人的成本为a万元. 已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为20万元的概率为0.
(Ⅰ)若不额外聘请工人,写出基地收益X的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
正确答案
(1)14.4;
(2)当额外聘请工人的成本高于1.6万元时,不外聘工人;成本低于1.6万元时,外聘工人;成本恰为1.6万元时,是否外聘工人均可以.
解析
本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
⑴解:设下周一有雨的概率为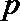
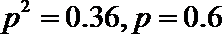
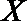
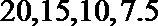
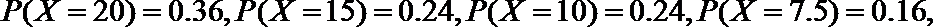
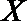

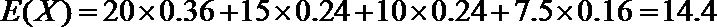
⑵设基地额外聘请工人时的收益为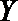
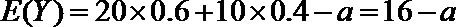
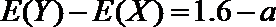
考查方向
本题考查了概率统计中的离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
1、写出随机变量的取值,并求出相应的概率和数学期望。
2、利用已知分类讨论。
易错点
随机变量的取值及对应的概率。
知识点
19.生产甲乙两种元件,其质量按检测指标划分为:
指标大于或者等于


(1)试分别估计元件甲,乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利



在(1)的前提下:
①记

②求生产

正确答案
(1)
(2)66.
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
解:(1)元件甲为正品的概率约为:
元件乙为正品的概率约为:
(2)①随机变量




而且


所以随机变量
所以:
②设生产的


依题意,
解得:
所以

设“生产


则:
考查方向
本题考查了概率统计中的离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点
解题思路
本题考查概率统计,解题步骤如下:
1、利用已知求出甲、乙为正品的概率。
2、写出随机变量的取值,并求出相应的概率和数学期望
易错点
随机变量的取值及对应的概率。
知识点
17. 某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为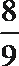
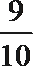
(I)求本月恰有两台仪器完全合格的概率;
(II)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为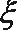
正确答案
解: (Ⅰ) 设恰有两台仪器完全合格的事件为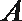
所以
(Ⅱ) 每月生产的仪器完全合格的台数可为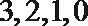
所以赢利额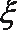
当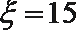
当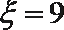
当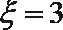
当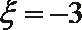
每月的盈利期望
所以每月的盈利期望值为
解析
见答案
考查方向
本题主要考查离散型随机变量的期望与方差,相互独立事件同时发生的概率,属于概率综合题,中档题。
解题思路
第1问直接用公式求解,第2问实际上求的是每月盈利的期望值。
易错点
计算能力弱
知识点
18.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,受到全国人民的瞩目。纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如下表所示:
(Ⅰ)若从抗战老兵中随机抽取2人进行座谈,求这2人参加纪念活动的环节数不同的概率;
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有

正确答案
见解析
解析
试题分析:本题属于概率中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对应取值的概率.
(Ⅰ)设“这2名抗战老兵参加纪念活动的环节数不同”为事件

根据题意可知
由对立事件的概率计算公式可得
故这2名抗战老兵参加纪念活动的环节数不同的概率为
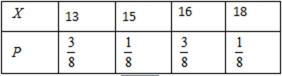
(Ⅱ)根据题意可知随机变量


则随机变量
则数学期望
考查方向
本题考查了离散型随机变量的概率分布列和数学期望,涉及到概率计算,是高考题中的高频考点.
解题思路
本题考查离散型随机变量的概率分布列和数学期望,解题步骤如下:
1、利用概率公式求解。
2、利用离散型随机变量的概率分布列和数学期望公式求解。
易错点
概率计算易错。
知识点
16.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分。 两人4局的得分情况如下:
(Ⅰ)若从甲的4局比赛中,随机选取2局,求这2局的得分恰好相等的概率;
(Ⅱ)如果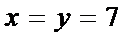
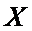
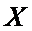
(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出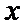
正确答案
(Ⅰ)
(Ⅱ)
(Ⅲ)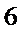

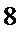
解析
试题分析:本题属于概率与统计的基本问题,题目的难点是逐渐由易到难,(1)直接按照步骤来求,(2)要注意正确求出每个变量对应的概率,(3)要注意利用离散型随机变量的分布列的性质验证分布列的正确性。
(Ⅰ)解:记 “从甲的4局比赛中,随机选取2局,且这2局的得分恰好相等”为事件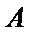
由题意,得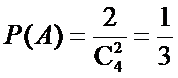
所以从甲的4局比赛中,随机选取2局,且这2局得分恰好相等的概率为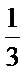
(Ⅱ)解:由题意,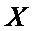
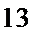
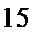
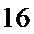

且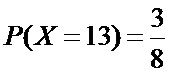
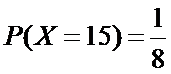
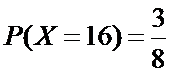
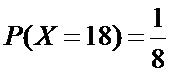
所以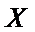
所以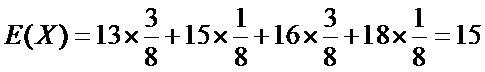
(Ⅲ)解: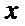
考查方向
本题主要考查了离散型随机变量的分布列、期望与方差,离散型随机变量的分布列大体有以下几类:
1.两点分布,
2.二项分布,超几何分布.
解题思路
本题考查离散型随机变量的分布列、期望与方差,解题步骤如下:
1.利用古典概型的概率公式进行求解;
2.写出随机变量的所有可能取值,分别求出每个变量对应的概率;
3.列表得到随机变量的分布列;
4.根据数学期望公式求其期望;
5.列出可能取值。
易错点
第二问中每个随机变量的概率不完全正确,导致结果错误。
知识点
18.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分. 两人4局的得分情况如下:
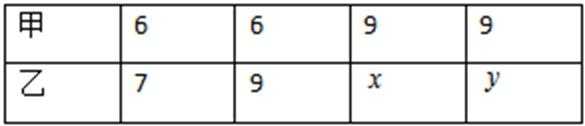
(Ⅰ)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求
(Ⅱ)如果




(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
正确答案
(Ⅰ)15
(Ⅱ)

(Ⅲ) 


解析
(Ⅰ)解:由题意,得

因为在乙的4局比赛中,随机选取1局,则此局得分小于6分的概率不为零,
所以
又因为

所以
所以
(Ⅱ)解:设 “从甲、乙的4局比赛中随机各选取1局,且得分满足
记甲的4局比赛为



为



则从甲、乙的4局比赛中随机各选取1局,所有可能的结果有16种, 它们是:















而事件








因此事件

(Ⅲ)解:



考查方向
解题思路
1、第一问由选取1局得分小于6分的概率不为零,可知x,y取值均为小于或等于5的自然数;结合乙的平均得分高于甲的平均得分确定的
2、第二问通过列举从甲、乙的4局比赛中随机各选取1局,所有可能的结果可以找出满足题意的事件数目,最终求出其概率。
3、第三问通过平均分相同得出

易错点
不能从题目中提取出

知识点
扫码查看完整答案与解析