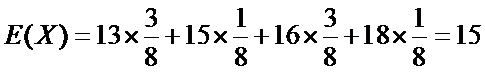- 离散型随机变量及其分布列、均值与方差
- 共180题
17.某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随
机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
(1)补全频率分布直方图(需写出计算过程);
(2)现从[40,55)岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组(每组3人)参加户外体验活动,记A组中年龄在[40,45)岁的人数为
求随机变量

正确答案
(1)0.06;
(2)
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
(1)因为第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3
所以高为0.3/5=0.06。频率直方图如下:
(2) 因为[40,45)组、[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,
所以三组中应抽出的人数分别为3、2、1.






考查方向
本题考查了概率统计中的频率分布直方图和离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
本题考查概率统计,解题步骤如下:
(1)利用直方图的性质求小矩形的高,并补充直方图。
(2)写出随机变量的取值,并求出相应的概率和数学期望。
易错点
(1)第一问中的高为频率/组距。
(2)第二问中随机变量的取值及对应的概率。
知识点
19.(1)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣 小组中按分层抽样的方法抽取50名同学(男

(1)能否据此判断有97.5% 的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5 — 7分钟,乙每次解答一道几何题所用的时间在6 - 8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率,
(3)现从选择做几何题的8名女生中
正确答案
(1)有97.5%的把握认为视觉和空间能力与性别有关;
(2)
(3)
解析
(1)由表中数据得K2的观测值
(2)设甲、乙解答一道几何题的时间分别为x、y分钟,则基本事件满足的区域为
设事件A为“乙比甲先做完此道题”则满足的区域为x>y,
∴由几何概型

(3)由题可知在选择做几何题的8名女生中任意抽取两人,抽取方法有






∴
考查方向
本题考查了独立性检验的应用;离散型随机变量的期望与方差.
解题思路
(1)根据所给的列联表得到求观测值所用的数据,把数据代入观测值公式中,做出观测值,同所给的临界值表进行比较,得到所求的值所处的位置,得到结论;
(2)利用面积比,求出乙比甲先解答完的概率;
(3)确定X的可能值有0,1,2.依次求出相应的概率求分布列,再求期望即可.
易错点
1、第一问中独立性检验知识不熟,公式不会应用;
2、第二问中几何概型转化成面积比
知识点
19.计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量
(Ⅰ)求在未来4年中,至多1年的年入流量超过120的概率;
(Ⅱ)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
若某台发电机运行,则该台发电机年利润为5000万元;若某台发电机未运行,则该台发电机年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
正确答案
(Ⅰ)
(Ⅱ)2
解析
(I)依题意


由二项分布,在未来4年中至多有1年入流量超过120的概率为:

(Ⅱ)记水电站年总利润为
由于水库年入流量总大于40,所以至少安装1台.
①安装1台发电机的情形:
由于水库年入流量总大于40,所以一台发电机运行的概率为1,
对应的年利润

②安装2台发电机的情形:
当

因此
当

因此
所以
所以
③安装3台发电机的情形:
当

因此
当

此时
当

因此
所以
所以
综上,欲使水电站年总利润的均值达到最大,应安装2台发电机.
考查方向
解题思路
(Ⅰ)先求出年入流量X的概率,根据二项分布,求出未来4年中,至少有1年的年入流量超过120的概率;
(Ⅱ)分三种情况进行讨论,分别求出一台,两台,三台的数学期望,比较即可得到.
易错点
第一问较简单,明确二项分布原理就不易出错,第二问分类出错
知识点
16.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分。 两人4局的得分情况如下:
(Ⅰ)若从甲的4局比赛中,随机选取2局,求这2局的得分恰好相等的概率;
(Ⅱ)如果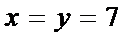
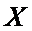
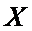
(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出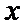
正确答案
(Ⅰ)
(Ⅱ)
(Ⅲ)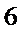

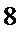
解析
试题分析:本题属于概率与统计的基本问题,题目的难点是逐渐由易到难,(1)直接按照步骤来求,(2)要注意正确求出每个变量对应的概率,(3)要注意利用离散型随机变量的分布列的性质验证分布列的正确性。
(Ⅰ)解:记 “从甲的4局比赛中,随机选取2局,且这2局的得分恰好相等”为事件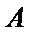
由题意,得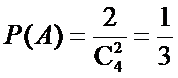
所以从甲的4局比赛中,随机选取2局,且这2局得分恰好相等的概率为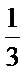
(Ⅱ)解:由题意,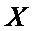
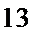
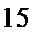

且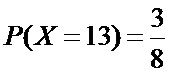
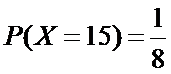
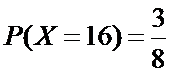
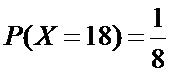
所以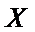
所以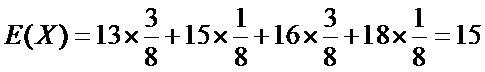
(Ⅲ)解: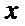
考查方向
本题主要考查了离散型随机变量的分布列、期望与方差,离散型随机变量的分布列大体有以下几类:
1.两点分布,
2.二项分布,超几何分布.
解题思路
本题考查离散型随机变量的分布列、期望与方差,解题步骤如下:
1.利用古典概型的概率公式进行求解;
2.写出随机变量的所有可能取值,分别求出每个变量对应的概率;
3.列表得到随机变量的分布列;
4.根据数学期望公式求其期望;
5.列出可能取值。
易错点
第二问中每个随机变量的概率不完全正确,导致结果错误。
知识点
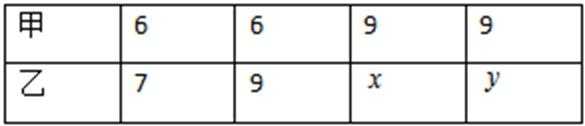
18.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分. 两人4局的得分情况如下:
(Ⅰ)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求
(Ⅱ)如果




(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
正确答案
(Ⅰ)15
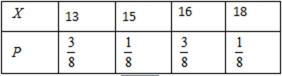
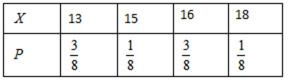
(Ⅱ)

(Ⅲ) 


解析
(Ⅰ)解:由题意,得

因为在乙的4局比赛中,随机选取1局,则此局得分小于6分的概率不为零,
所以
又因为

所以
所以
(Ⅱ)解:设 “从甲、乙的4局比赛中随机各选取1局,且得分满足
记甲的4局比赛为



为



则从甲、乙的4局比赛中随机各选取1局,所有可能的结果有16种, 它们是:















而事件








因此事件

(Ⅲ)解:



考查方向
解题思路
1、第一问由选取1局得分小于6分的概率不为零,可知x,y取值均为小于或等于5的自然数;结合乙的平均得分高于甲的平均得分确定的
2、第二问通过列举从甲、乙的4局比赛中随机各选取1局,所有可能的结果可以找出满足题意的事件数目,最终求出其概率。
3、第三问通过平均分相同得出

易错点
不能从题目中提取出

知识点
扫码查看完整答案与解析