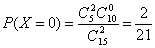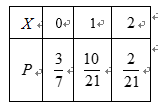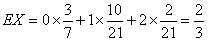离散型随机变量及其分布列、均值与方差
共180题

离散型随机变量及其分布列、均值与方差
共180题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

17.空气质量指数 (单位:)表示每立方米空气中可入肺颗粒物的含量，这

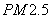
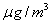
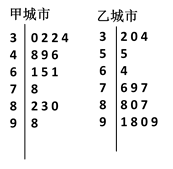
个值越高，就代表空气污染越严重：

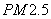
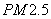
甲、乙两城市2013年2月份中的15天对空气质量指数进行监测，获得

日均浓度指数数据如茎叶图所示:

（1）根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?

(注：不需说明理由)

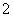
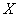
（2）在乙城市15个监测数据中任取个，设为空气质

量类别为优或良的天数，求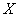的分布列及数学期望。

正确答案

见解析。

解析

（1）甲城市空气质量总体较好，

（2）的取值为，

，，

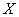
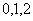
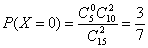
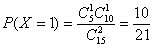
所以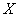的分布列为：

数学期望

知识点

离散型随机变量及其分布列、均值与方差茎叶图

题型：简答题

简答题 · 13 分

正确答案

见解析

解析

（1）由题意可知，，，，

∴

（2）先用反证法证明：

若

则，∴

同理可知，∴

由题目所有数和为

即

∴

与题目条件矛盾

∴。

易知当时，存在

∴的最大值为1

（3）的最大值为.

首先构造满足的：

，

经计算知，中每个元素的绝对值都小于1，所有元素之和为0，且

，

下面证明是最大值. 若不然，则存在一个数表，使得.

由的定义知的每一列两个数之和的绝对值都不小于，而两个绝对值不超过1的数的和，其绝对值不超过2，故的每一列两个数之和的绝对值都在区间中. 由于，故的每一列两个数符号均与列和的符号相同，且绝对值均不小于.

设中有列的列和为正，有列的列和为负，由对称性不妨设，则. 另外，由对称性不妨设的第一行行和为正，第二行行和为负。

考虑的第一行，由前面结论知的第一行有不超过个正数和不少于个负数，每个正数的绝对值不超过1（即每个正数均不超过1），每个负数的绝对值不小于（即每个负数均不超过）. 因此

，

故的第一行行和的绝对值小于，与假设矛盾. 因此的最大值为。

知识点

离散型随机变量及其分布列、均值与方差

题型：简答题

简答题 · 12 分

PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方以下空气质量为一级；在35微克/立方米~75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标.

某市环保局从360天的市区PM2.5监测数据中，随机抽取15天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）.

（1）从这15天的数据中任取3天的数据，记表示空气质量达到一级的天数，求的分布列；

（2）以这15天的PM2.5日均值来估计这360天的空气质量情况，则其中大约有多少天的空气质量达到一级.

正确答案

见解析。

解析

知识点

离散型随机变量及其分布列、均值与方差茎叶图

题型：单选题

单选题 · 5 分

一个篮球运动员投篮一次得3分的概率为a，得2分的概率为b，不得分的概率为，已知他投篮一次得分的期望是2，则的最小值为

正确答案

解析

略

知识点

利用基本不等式求最值离散型随机变量及其分布列、均值与方差

题型：简答题

简答题 · 12 分

某公司为招聘新员工设计了一个面试方案:应聘者从道备选题中一次性随机抽取道题,按照题目要求独立完成，规定:至少正确完成其中道题的便可通过，已知道备选题中应聘者甲有道题能正确完成,道题不能完成；应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响。

（1）分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望；

（2）请分析比较甲、乙两人谁的面试通过的可能性大？

正确答案

见解析

解析

（1）设甲正确完成面试的题数为, 则的取值分别为， ………1分

；

； ………3分

考生甲正确完成题数的分布列为

， ………………4分

设乙正确完成面试的题数为，则取值分别为， ………………5分

；

， ………………7分

考生乙正确完成题数的分布列为:

， ………………8分

（2）因为, ……………10分

， ……12分

（或）。

所以。

（或：因为,,

所以， )

综上所述，

从做对题数的数学期望考查,两人水平相当；

从做对题数的方差考查,甲较稳定；

从至少完成道题的概率考查,甲获得面试通过的可能性大， ……………13分

知识点

古典概型的概率离散型随机变量及其分布列、均值与方差

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 离散型随机变量及其分布列、均值与方差

扫码查看完整答案与解析