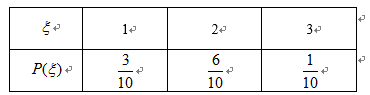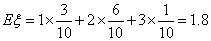- 离散型随机变量及其分布列、均值与方差
- 共180题
李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有






(1)若走
(2)若走
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
正确答案
见解析
解析
知识点
为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下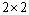
(1)根据独立性检验的基本思想,约有多大的把握认为“性别与喜欢数学课之间有关系”?
(2)若采用分层抽样的方法从不喜欢数学课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为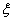
正确答案
见解析。
解析
(1)∵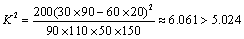
∴约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
(2)男生抽取的人数有: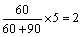
女生抽取的人数各有: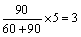
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,
所以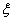
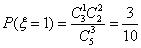
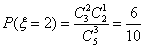
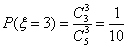
所以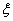
所以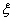
知识点
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: 



(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为

正确答案
见解析。
解析
(1)由题意得,分数在

所以样本人数为


(2)从分组区间和频数可知,样本众数的估计值为
由(1)知分数在
所以频率分布直方图中
(3)成绩不低于80分的样本人数为4+2=6(人),成绩在90分以上(含90分)的人数为




所以
所以
知识点
某大型公益活动从一所名牌大学的四个学院中选出了
(1)若从这
(2)现要从这




正确答案
见解析。
解析
(1)设“两名学生来自同一学院”为事件
则
即两名学生来自同一学院的概率为
(2) 







所以
…………………………………………………………………11分
所以
知识点
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高,现从一批数量很大的罗非鱼中随机地抽出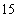
《中华人民共和国环境保护法》规定食品的汞含量不得超过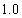
(1)检查人员从这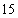
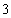
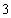
(2)若从这批数量很大的鱼中任选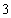
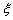

正确答案
见解析
解析
(1)记“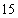
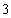
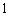
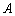
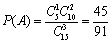
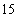
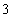
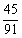
(2)依题意可知,这批罗非鱼中汞含量超标的鱼的概率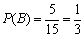
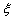
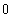
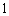
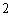
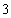
则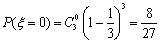
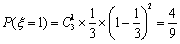
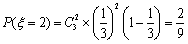
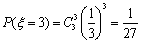
其分布列如下:
…………………………12分
所以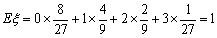
知识点
扫码查看完整答案与解析