- 离散型随机变量及其分布列、均值与方差
- 共180题
甲、乙两人参加某种选拔测试,在备选的







(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率。
正确答案
见解析
解析
(1)解:设乙答题所得分数为






乙得分的分布列如下:

(2)解:由已知甲、乙至少答对


则

故甲乙两人至少有一人入选的概率
知识点
某公司准备将100万元资金投入代理销售业务,现有A,B两个项目可供选择:
投资A项目一年后获得的利润X1(万元)的概率分布列如下表所示:
且X1的数学期望E(X1)=12;
投资B项目一年后获得的利润X2(万元)与B项目产品价格的调整有关, B项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p(0< p <1)和1p. 经专家测算评估:B项目产品价格一年内调整次数X(次)与X2的关系如下表所示:
(1)求a,b的值;
(2)求X2的分布列;
(3)若E(X1)< E(X2),则选择投资B项目,求此时 p的取值范围.
正确答案
(1)
(2)
(3)
解析
(1)由题意得:
解得:
(2)X2 的可能取值为



所以X2的分布列为:
……………………………………9分
(3)由(2)可得:

因为E(X1)< E(X2),
所以
所以
当选择投资B项目时,

知识点
某工厂在试验阶段大量生产一种零件,这种零件有甲、乙两项技术指标需要检测,设各项技术指标达标与否互不影响,按质量检验规定:两项技术指标都达标的零件为合格品,为估计各项技术的达标概率,现从中抽取1000个零件进行检验,发现两项技术指标都达标的有600个,而甲项技术指标不达标的有250个。
(1)求一个零件经过检测不为合格品的概率及乙项技术指标达标的概率;
(2)任意抽取该零件3个,求至少有一个合格品的概率;
(3)任意抽取该种零件4个,设ξ表示其中合格品的个数,求随机变量ξ的分布列。
正确答案
见解析。
解析
(1)记一个零件中甲项技术达标的事件为A,乙项技术达标的事件为B
由题意可得,两项技术都达标的概率为P(AB)=
甲项技术不达标的概率P(

因此一个零件经过检测不合格的概率为1﹣P(AB)=1﹣
由独立性可知,P(AB)=P(A)P(B)
∴P(B)=

即乙项技术指标达标的 概率为
(2)任意抽取该种零件3个,至少有一个合格品的概率1﹣
(3)随机变量ξ的可能取值为0,1,2,3,4
P(ξ=0)=
P(ξ=1)=
P(ξ=2)=
P(ξ=3)=
P(ξ=4)=
∴ξ的分布列为
知识点
空气质量指数

甲、乙两城市2013年2月份中的15天对空气质量指数

(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(2)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(3) 在乙城市15个监测数据中任取


正确答案
见解析
解析
(1)甲城市空气质量总体较好. ………2分
(2)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为
乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为
在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率为
………8分
(3)




数学期望
知识点
甲、乙、丙三名优秀的大学毕业生参加一所重点中学的招聘面试,面试合格者可以签约。甲表示只要面试合格就签约,乙与丙则约定,两个面试都合格就一同签约,否则两人都不签约。设每个人面试合格的概率都是P,且面试是否合格互不影响。已知至少有1人面试合格概率为
(1)求P。
(2)求签约人数
正确答案
见解析。
解析
解:
(1)至少1人面试合格概率为


(2)签约人数

甲不合格,乙丙至少一人不合格



签约人数为0的概率:





签约人数为2的概率:甲不合格,乙丙全部合格:

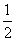
签约人数为3的概率:甲乙丙均合格:
分布表:
数学期望:
知识点
扫码查看完整答案与解析
































