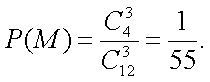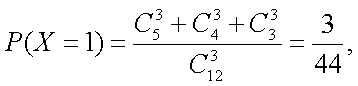- 离散型随机变量及其分布列、均值与方差
- 共180题
在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某明星判断正确的概率为



(1)当


(2)当

正确答案
见解析
解析
(1)

故

所以 ξ的分布列为:
且



(2)当S8=2时,即答完8题后,回答正确的题数为5题,回答错误的题数是3题,
又已知
此时的概率为
知识点
某品牌汽车4
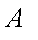
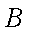

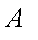
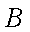
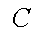
(1)求该单位购买的3辆汽车均为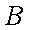
(2)记该单位购买的3辆汽车的排量种数为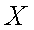
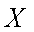
正确答案
见解析。
解析
(1)设该单位购买的3辆汽车均为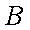
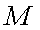
所以该单位购买的3辆汽车均为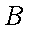
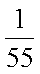
(2)随机变量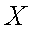
所以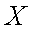
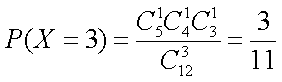
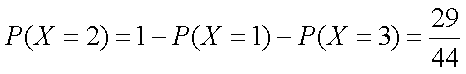
所以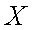
数学期望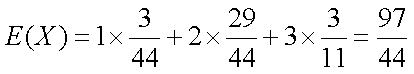
知识点
第30届夏季奥运会将于2012年7月27日在伦敦举行, 当地某学校招募了8名男志愿者和12名女志愿者. 将这20名志愿者的身高编成如下茎叶图(单位:cm):
若身高在180cm以上(包括180cm)定义为“高个子”, 身高在180cm以下(不包括180cm)定义为“非高个子”, 且只有“女高个子”才能担任“礼仪小组”.
(1) 如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人, 再从这5人中选2人, 那么至少有一人是“高个子”的概率是多少?
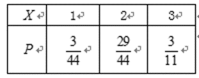
(2) 若从所有“高个子”中选3名志愿者, 用X表示所选志愿者中能担任“礼仪小组”的人数, 试写出X的分布列, 并求X的数学期望.
正确答案
(1)
解析
解析:
知识点
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数
正确答案
见解析。
解析
(1)设甲同学在5次投篮中,有


=

(2)由题意








知识点
某商场在节日期间搞有奖促销活动,凡购买一定数额的商品,就可以摇奖一次,摇奖办法是在摇奖机中装有大小、质地完全一样且分别标有数字1~9的九个小球,一次摇奖将摇出三个小球,规定:摇出三个小球号码是“三连号”(如1、2、3)的获一等奖,奖1000元购物券;若三个小球号码“均是奇数或均是偶数”的获二等奖,奖500元购物券;若三个小球号码中有一个是“8”的获三等奖,奖200元购物券;其他情形则获参与奖,奖50元购物券,所有获奖等第均以最高奖项兑现,且不重复兑奖,记X表示一次摇奖获得的购物券金额。
(1)求摇奖一次获得一等奖的概率;
(2)求X的概率分布列和数学期望。
正确答案
见解析。
解析
(1)记“摇奖一次获得一等奖”为事件A,
连号的可能情况有:123,234,345,456,567,678,789共7种情况。
∴P(A)=


故摇奖一次获得一等奖的概率为
(2)由题设知X的可能取值分别为1000,500,200,50。
P(X=1000)=


P(X=200)=

P(X=50)=


∴X的分布列如下:
EX=

知识点
扫码查看完整答案与解析