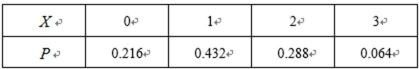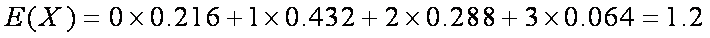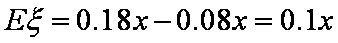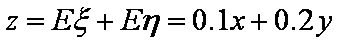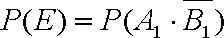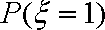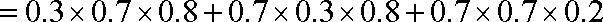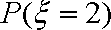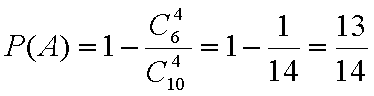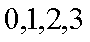- 离散型随机变量及其分布列、均值与方差
- 共180题
盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同。
(1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为


正确答案
见解析。
解析
(1)一次取2个球共有

∴取出的2个球颜色相同的概率
(2)X的所有可能取值为
∴X的概率分布列为
故X的数学期望
知识点
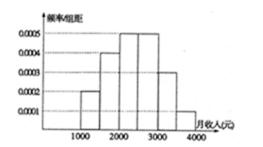
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500) 单位:元)
(1)估计居民月收入在[1500,2000)的概率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在[2500,3500)的居民数X的分布和数学期望。
正确答案
见解析。
解析
(1)依题意及频率分布直方图知,居民月收入在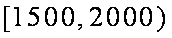
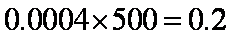
(2)频率分布直方图知,中位数在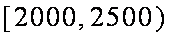
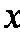
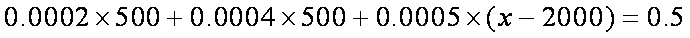
解得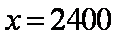
(3)居民月收入在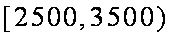
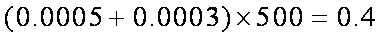
由题意知,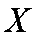
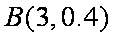
因此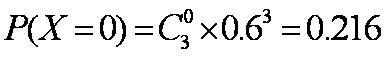
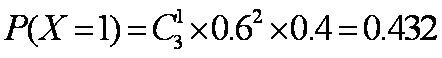
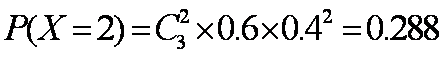
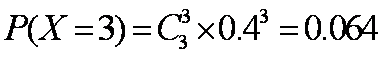
故随机变量X的分布列为
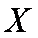
知识点
我国政府对PM2。5采用如下标准:
某市环保局从180天的市区PM2。5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)。
(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记

(3)以这10天的PM2。5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级。
正确答案
见解析
解析
(1)10天的中位数为(38+44)/2=41(微克/立方米) ·············2分
(2)由 

利用

··············10分
(3)一年中每天空气质量达到一级的概率为



知识点
据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
假设投资A项目的资金为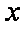
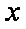
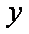
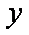

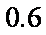
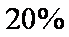
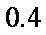
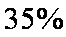
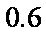
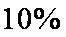
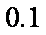
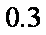
(1)记投资A,B项目的利润分别为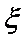
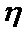
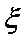
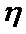
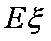
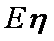
(2)某公司计划用不超过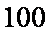

正确答案
(1)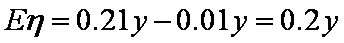
解析
(1)A项目投资利润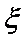
B项目投资利润
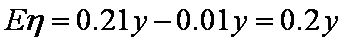
(2)由题意可知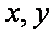
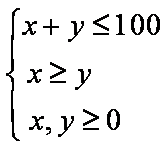
由(1)可知,
当
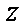
∴对A、B项目各投资50万元,可使公司获得最大利润,最大利润是15万元.…………12分
知识点
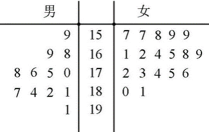
某航空公司进行空乘人员的招聘,记录了前来应聘的6名男生和9名女生的身高,数据用茎叶图表示如图(单位:cm),应聘者获知:男性身高在区间[174,182],女性身高在区间[164,172]的才能进入招聘的下一环节。
(1)求6名男生的平均身高和9名女生身高的中位数;
(2)现从能进入下一环节的应聘者中抽取2人,记X为抽取到的男生人数,求X的分布列及期望。
正确答案
见解析
解析
(1)6名男生的平均身高为
(2)男性身高在区间[174,182]的有176、178、180;女性身高在区间[164,172]的166,167,168,170,则
X的可能取值为0,1,2,所以
P(X=0)=




X的分布列为
期望为0×


知识点
公安部最新修订的《机动车驾驶证申领和使用规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二),只有三个科目都过关后才能拿到驾驶证,某驾校现有100名新学员,第一批参加考试的20人各科目通过的人数情况如下表:
请你根据表中的数据:
(1)估计该驾校这100名新学员有多少人一次性(不补考)获取驾驶证;
(2)第一批参加考试的20人中某一学员已经通过科目一的考试,求他能通过科目二却不能通过科目三的概率;
(3)该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元,现从这20人中随机抽取1人,记X为学校因为该学员而奖励教官的金额数,求X的数学期望。
正确答案
见解析
解析
(1)由表中数据可知一次性(不补考)获取驾驶证的频率为
估计这100名新学员中有100×
(2)设“通过科目一、二、三”分别为事件A,B,C,则P=P(B

(3)设这个学员一次性过关的科目数为Y,则Y的分布列为
EY=0×




而X=100Y,所以EX=100EY=100×
知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为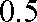



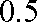
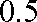
(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为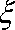
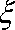
正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件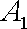
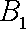
设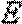
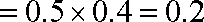
(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:
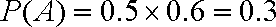
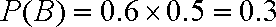
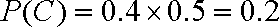
(3)经过前后两次选拔后合格入选的人数为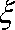
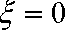
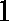
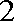

则,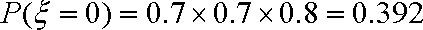
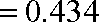
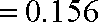
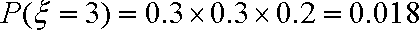
则,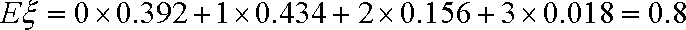
知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为





(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为


正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件

设

(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:



(3)经过前后两次选拔后合格入选的人数为




则,



则,
知识点
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设甲比赛的次数为

正确答案
见解析。
解析
记甲


(1)比赛三局甲获胜的概率是:
(2)比赛四局甲获胜的概率是:
比赛五局甲获胜的概率是:
甲获胜的概率是:
(3)记乙





故甲比赛次数的分布列为:
所以甲比赛次数的数学期望是:

知识点
某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
(2)若从所有“运动健将”中选3名代表,用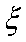
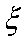
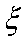
正确答案
见解析
解析
(1)根据茎叶图,有“运动健将”12人,“运动积极分子”18人
用分层抽样的方法,每个人被抽中的概率为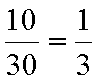
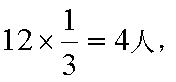
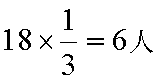
设事件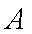
(2)由茎叶图知男“运动健将有”8人,女“运动健将”有4人,故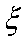
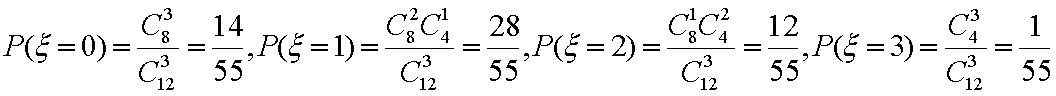

知识点
扫码查看完整答案与解析