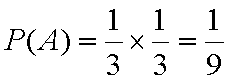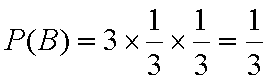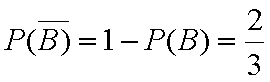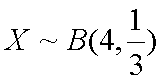- 离散型随机变量及其分布列、均值与方差
- 共180题
选聘高校毕业生到村任职,是党中央作出的一项重大决策,这对培养社会主义新农村建设带头人、引导高校毕业生面向基层就业创业,具有重大意义。为了响应国家号召,某大学决定从符合条件的6名(其中男生4人,女生2人)报名大学生中选择3人,到某村参加村委会主任应聘考核。
(1)设所选3人中女生人数为

(2)在男生甲被选中的情况下,求女生乙也被选中的概率。
正确答案
见解析。
解析
(1)
依题意得:


∴
∴ 
(2)设“男生甲被选中”为事件

则

∴
故在男生甲被选中的情况下,女生乙也被选中的概率为
知识点
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85), 第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ) 学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有

正确答案
见解析
解析
解:(1)第三组的频率为0.06
第四组的频率为0.04
第五组的频率为0.02
(2)(ⅰ)设M:学生甲和学生乙同时进入第二轮面试
P(M)=

(ⅱ)

知识点
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分剐为1,2,3,4,从袋中任意取出3个球。
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望。
正确答案
见解析
解析
解:(1)设“取出的3个球编号都不相同”为事件A,设“取出的3个球恰有两个编号相同”为事件B,
则P(B)=


∴P(A)=1﹣P(B)=
答:取出的3个球编号都不相同的概率为
(2)X的取值为1,2,3,4。
P(X=1)=

P(X=2)=

P(X=3)=

P(X=4)=

所以X的分布列为:
X的数学期望EX=1×




知识点
为了响应学校“学科文化节”活动,数学组举办了一场数学知识比赛,共分为甲、乙两组,其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生,现从得满分的学生中,每组各任选2个学生,作为数学组的活动代言人。
(1)求选出的4个学生中恰有1个女生的概率;
(2)设

正确答案
见解析
解析
解析:(1)设“从甲组内选出的2个同学均为男同学;从乙组内选出的2个同学中,1个是男同学,1个为女同学”为事件



∴选出的4个同学中恰有1个女生的概率为

(2)
∴
…………10分
∴

知识点
某产品按行业生产标准分成







(1)从该厂生产的产品中随机抽取
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数


(2)已知该厂生产一件该产品的利润y(单位:元)与产品的等级系数



正确答案
见解析
解析
解析:(1)由样本数据知,30件产品中等级系数
∴样本中一等品的频率为

二等品的频率为

三等品的频率为

(2)∵
用样本的频率分布估计总体分布,将频率视为概率,由(1)可得


∴可得
其数学期望
知识点
宿州市医疗保险实行定点医疗制度,按照“就近就医,方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构。若甲、乙、丙、丁4名参加保险人员所在的地区附近有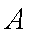

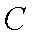
(1)求甲、乙两人都选择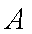
(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设4名参加保险人员中选择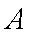

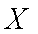
正确答案
见解析。
解析
(1)设“甲、乙两人都选择A社区医院”为事件A,那么
∴甲、乙两人都选择A社区医院概率为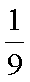
(2)设“甲、乙两人选择同一社区医院”为事件B,那么
∴甲、乙两人不选择同一社区医院的概率是
(3)依题意
∴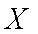
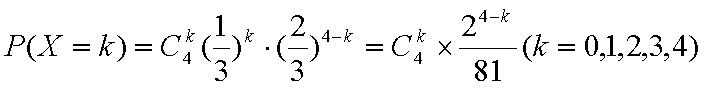
∴
知识点
10.已知P为双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机
抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果,
其中某班级的正确率为



(1) 求

(2)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.将10个白小球中的3个染成红色,3个染成黄色,试解决下列问题:
(1)求取出3个小球中红球个数
(2)求取出3个小球中红球个数多于白球个数的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为

(1)求甲乙二人中至少有一人破译出密码的概率;
(2)求
(3)设甲、乙、丙三人中破译出密码的人数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析