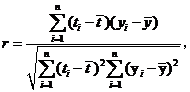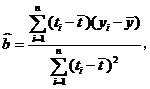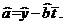- 线性回归方程
- 共28题
18.
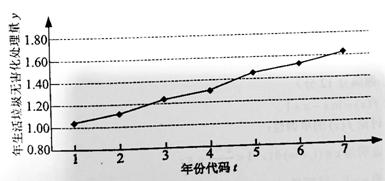
下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图。
注:年份代码1~7分别对应年份2008~2014.
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: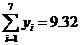
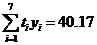
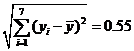
参考公式:
回归方程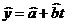
正确答案
(Ⅰ)由折线图中数据和附注中参考数据得
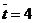
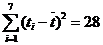
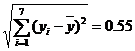
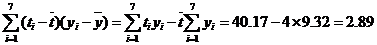
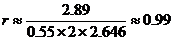
因为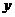
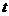
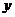
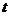
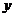
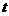
(Ⅱ)由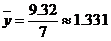
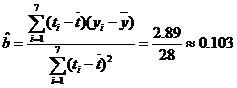
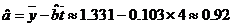
所以,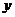
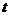
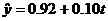
将2016年对应的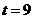
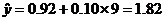
所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨. .........12分
知识点
5.某洗发水的广告费用x与销售额y的统计数据如下表所示,根据表中数据可得回归方程

正确答案
解析
由表中数据得:


从而线性回归方程为


由表中数据得:


从而线性回归方程为


考查方向
解题思路
根据回归直线方程过样本的中心点即可解出。
易错点
不知道考查的知识点是什么。
知识点
5.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,收集数据如右表示:根据右表可得回归方程

正确答案
解析
由题中给出的表格得





考查方向
解题思路
先求出样本点的中心

易错点
不知道回归直线过样本点的中心,误将表格中的点带入回归直线导致出错运算结果出错。
知识点
13.给出下列命题:
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②由变量x和y的数据得到其回归直线方程L:y =bx + a,则L一定经过点P(x,y)
③从匀速传递的产品生产流水线上


④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
⑤在回归直线方程y = 0.lx + 10中,当解释变量x每增加一个单位时,预报变量y增加0.1 个单位,
其中真命题的序号是 .
正确答案
②④⑤
解析
①线性相关系数|r|越大,两个变量的线性相关性越强,故①不正确;
②由变量x和y的数据得到其回归直线方程l:y=bx+a,则l一定经过点P故②正确;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样不是分层抽样,故③不正确;
④可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故④正确;
⑤在回归直线方程y=0.1x+10中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位,故⑤正确.
故答案为:②④⑤
考查方向
本题线性相关、回归直线方程和拟合等相关概念。
易错点
对上述概念理解的不透彻
知识点
5.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
由此表可得回归直线方程
正确答案
解析




考查方向
本题主要考查了回归直线方程/在高考中不经常考查,主要考查用回归方程预测、样本中心、散点图。
解题思路
易错点
忽视回归直线经过样本中心,而用公式去求
知识点
扫码查看完整答案与解析