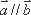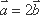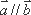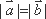- 平面与平面平行的判定与性质
- 共195题
如图,四棱柱










(1)证明:

(2)求此四棱柱被平面
(3)若


求平面

正确答案
见解析。
解析
本题以直四棱柱为背景,考察学生的空间意识、运算和推演能力,考查空间整合思想的运用。
(1)取AD中点M,AA1中点N,连MN,MC,NQ。则MN‖A1D,又QC‖A1D,则MN‖QC,由于四棱柱


BC=AM,则∆AMN
(2)若AB,CD交于点E,则A1Q过点E,若∆BCE面积为s,则四边形





(3)过A作AH⊥CD于H,连A1H,则∠A1HA为平面





所以,平面


知识点
设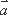
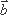
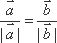
正确答案
解析
若使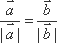

知识点
若实数


正确答案
解析
知识点
已知函数f(x)=lnx﹣ax2+(2﹣a)x。
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x<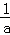
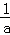
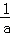
(3)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f′( x0)<0。
正确答案
见解析
解析
(1)函数f(x)的定义域为(0,+∞),
f′(x)=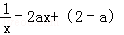
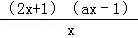
①若a>0,则由f′(x)=0,,得x=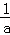
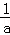
当x∈(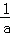
所以f(x)在(0,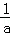
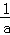
②当a≤0时,(x)>0恒 成立,因此f(x)在(0,+∞)单调递增;
(2)设函数g(x)=f(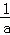
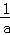
g′(x)=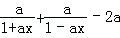
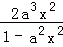
当x∈(0,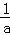
所以g(x)>0,
故当0<x<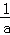
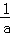
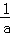
(3)由(1)可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,
故a>0,从而f(x)的最大值为f(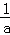
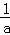
不妨设A(x1,0),B(x2,0),0<x1<x2,
则0<x1<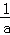
由(2)得,f(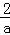
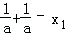
从而f(x)在(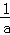
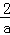
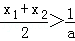
由(1)知,f′( x0)<0。
知识点
如图,在正方体






正确答案
90º
解析
方法一:连接D1M,易得DN⊥A1D1 ,DN⊥D1M,
所以,DN⊥平面A1MD1,
又A1M
方法二:以D为原点,分别以DA, DC, DD1为x, y, z轴,建立空间直角坐标系D—xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2)
故,
所以,cos<
知识点
扫码查看完整答案与解析