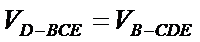- 平面与平面平行的判定与性质
- 共195题
如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=
34.求平面PAB与平面PCD所成二面角的余弦值;
35.点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
正确答案
解析
以A为坐标原点,以AB、AD、AP所在直线分别为x、y、z轴建系A﹣xyz如图,
由题可知B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
(1)∵AD⊥平面PAB,∴
∵

设平面PCD的法向量为
由

取y=1,得
∴cos<



∴平面PAB与平面PCD所成两面角的余弦值为
考查方向
解题思路
(1)所求值即为平面PAB的一个法向量与平面PCD的法向量的夹角的余弦值的绝对值,计算即可;
易错点
本题考查求二面角的三角函数值,在计算过程中易错。
正确答案
解析
(2)∵


又



又




设1+2λ=t,t∈[1,3],
则cos2<




当且仅当t=




因为y=cosx在(0,
又∵BP=



考查方向
解题思路
(2)利用换元法可得cos2<



易错点
本题考查求二面角的三角函数值,考查用空间向量解决问题的能力,在求最值时易错.
如图,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
求证:
19.DE∥平面AA1C1C;
20.BC1⊥AB1.
正确答案
(1)根据题意,得;E为B1C的中点,D为AB1的中点,所以DE∥AC;又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C;
解析
(1)根据题意,得;E为B1C的中点,D为AB1的中点,所以DE∥AC;又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C;
考查方向
解题思路
根据中位线定理得DE∥AC,即证DE∥平面AA1C1C;
正确答案
(2)因为棱柱ABC﹣A1B1C1是直三棱柱,所以CC1⊥平面ABC,
因为AC⊂平面ABC,所以AC⊥CC1;
又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,
BC∩CC1=C,所以AC⊥平面BCC1B1;又因为BC1⊂平面平面BCC1B1,
所以BC1⊥AC因为BC=CC1,所以矩形BCC1B1是正方形,
所以BC1⊥平面B1AC;又因为AB1⊂平面B1AC,
所以BC1⊥AB1.
解析
间答案
考查方向
解题思路
先由直三棱柱得出CC1⊥平面ABC,即证AC⊥CC1;再证明AC⊥平面BCC1B1,即证BC1⊥AC;最后证明BC1⊥平面B1AC,即可证出BC1⊥AB1.
易错点
本题考查了直线与直线,直线与平面以及平面与平面的位置关系,也考查了空间想象能力和推理论证能力的应用问题,在严格应用定理过程中易错.
7.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为
正确答案
解析
由已知可知SC垂直面ABC,
且底面三角形ABC中AC=4,AC边上的高为
故BC=4,在直角三角形SBC中,由SC=4
可得
考查方向
简单空间图形的三视图
解题思路
由已知中的三视图可得SC垂直平面ABC,进而根据勾股定理得到答案
易错点
计算能力弱,空间立体感不强
知识点
如图,四棱锥







22.求证:面

23.设






正确答案
(1)证明:由


有





因为




解析
在梯形ABCD中,BC⊥BD,BC⊥PD,所以BC⊥平面PBD。又BC在平面PBC内,所以PBC⊥平面PBD.
考查方向
考查”两个平面互相垂直的判定定理:若一个平面过另一个平面的垂线,则这两个平面垂直。"
解题思路
根据已知条件及思路,需要在平面PBC内找到一条直线垂直于平面PBD。易证BC⊥BD,BC⊥PD,则得到BC⊥平面PBD。
易错点
难以找到一条直线垂直于另一个平面,或发现了垂直关系,但没有严格证明出现错误。
教师点评
此题考查了证明两个平面垂直的方法,是通过线面垂直而得到的。借此类题,要善于发现垂直关系。
正确答案
由(1)可知


∴



可得

以



设平面

则

设平面

则

所以


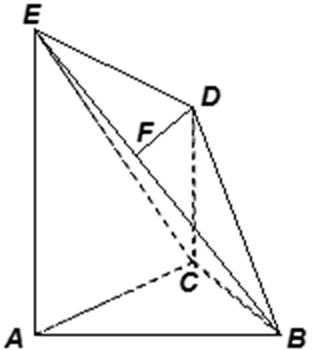
在如图所示的几何体中,平面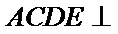
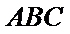
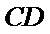
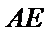
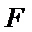
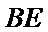
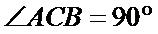
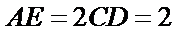
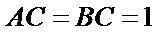
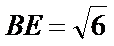
18.求证: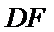
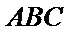
19.求证:
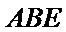
20.求三棱锥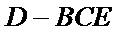
正确答案
证明:设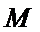
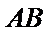

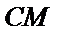
在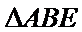
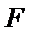
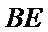
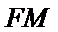
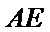
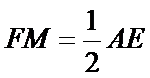
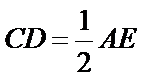
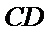
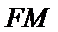
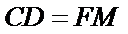
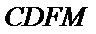
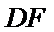
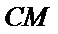
因为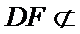
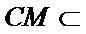
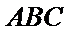
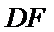
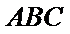

解析
证明:设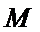
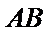

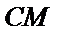
在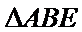
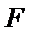
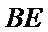
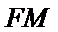
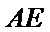
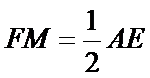
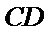
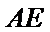
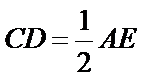
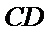
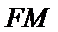
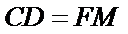
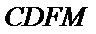
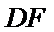
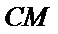
因为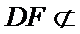
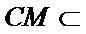
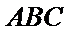
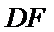
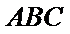

考查方向
直线和平面平行的判定
解题思路
取AB的中点,连接FM和CM,利用三角形中位线和平行线的性质,推导出线面平行成立的条件。
易错点
证明出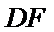
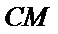
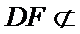
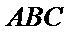
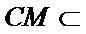
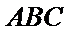
教师点评
本题考察学生做辅助线的能力,考查学生对三角形中位线,平行四边形的性质,以及直线与平面平行的判定定理的掌握程度。
正确答案
解:在直角三角形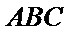
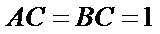
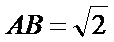
因为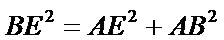
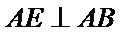
已知平面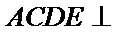
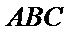
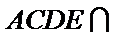
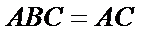
又因为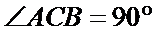

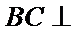
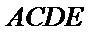
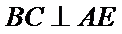
又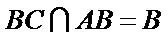
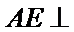
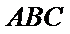
因为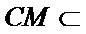
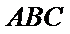
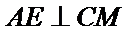
在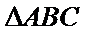
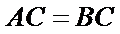
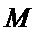
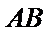
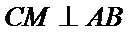
又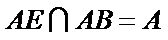
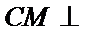
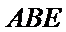
由(Ⅰ)知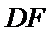
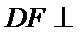

解析
解析:在直角三角形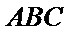
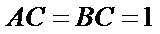
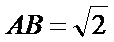
因为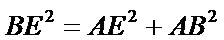
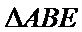
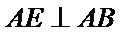
已知平面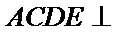
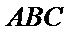
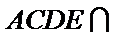
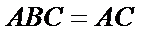
又因为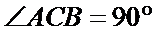

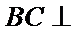
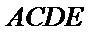
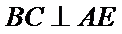
又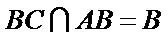
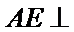
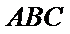
因为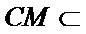
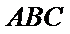
在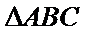
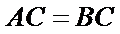
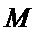
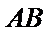
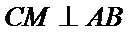
又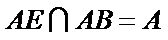
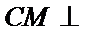
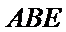
由(Ⅰ)知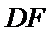
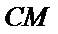
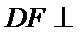

考查方向
直线与平面垂直的判定与性质。
解题思路
分别在三角形ABC和三角形ABE中应用勾股定理证明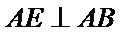
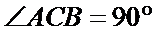
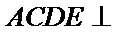
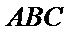
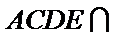
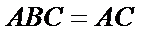
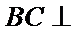
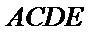
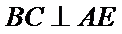
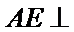
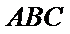
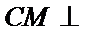
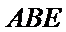
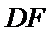
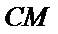
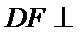
易错点
由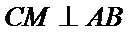
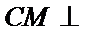
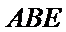
教师点评
本题难度中等,过程复杂,既考查了平面几何知识在立体几何中的灵活应用,又考察了直线和平面平行的判定和性质定理的应用。
正确答案
解:由(Ⅱ)知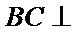
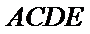
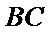
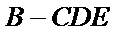
所以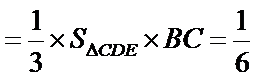
解析
解析:由(Ⅱ)知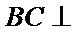
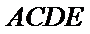
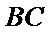
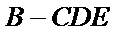
所以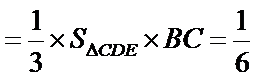
考查方向
棱锥的体积公式
解题思路
三棱锥可以把任何一个面作为底,顶点到底面的距离作为高。这里把三角形CDE做底,BC做高,容易计算体积。
易错点
把BCE作为三棱锥的地面,很难求出高。
教师点评
本题考察学生对三棱锥体积公式的灵活运用。
扫码查看完整答案与解析