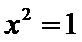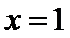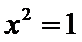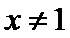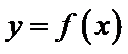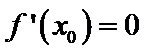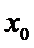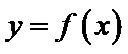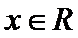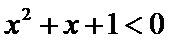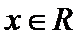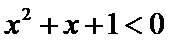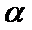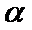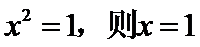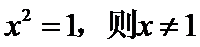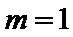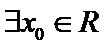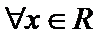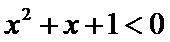- 含有逻辑联结词命题的真假判断
- 共52题
4.下列结论正确的是( )
正确答案
解析
根据否命题是条件结论全否,所以A错。
特例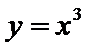
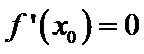
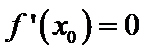
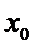
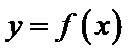
特称命题的否定是全称命题,且否定结论,所以C错
命题“
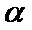
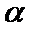
考查方向
解题思路
1)否命题是条件结论全否,命题的否定是只否定结论,对A C D进行选择
2)使用充分,必要条件的判定对BC进行排除
易错点
本题易错于否命题和命题的否定的区别,导致无法排除
知识点
5.已知命题







正确答案
解析




考查方向
解题思路
分别判断命题p,q的真假, 再分析复合命题的真假
易错点
复合命题的真值判断易出错
知识点
3.下列有关命题的说法正确的是
正确答案
解析
命题“若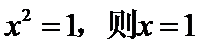
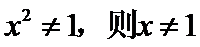

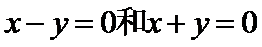
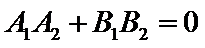
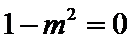

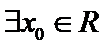
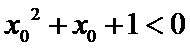
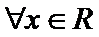
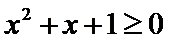
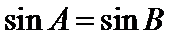
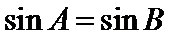
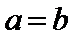
考查方向
解题思路
1)否命题的定义是否定题设和结论;
2)两直线垂直的充要条件是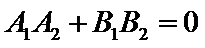
3)特称命题的否定是将特称改为全称,否定结论;
4)逆命题是题设和结论互换,然后判断若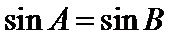
易错点
本题易在判定命题的否定和否命题时出现错误,以及判断必要条件时出现错误,两直线垂直的充要条件用错,三角形中角和正弦值之间的关系也易错。
知识点
10.若





正确答案
解析
由















考查方向
解题思路
1.先根据题中给出的条件求出函数

易错点
1.三角函数的基础知识记不住导致出错;2.不考虑函数的单调性直接将0,
知识点
4.下列说法中正确的是( )
正确答案
解析








考查方向
解题思路
1.奇函数是否过
易错点
本题易在判定命题的否定和否命题时出现错误,以及判断必要条件时出现错误,三角形中角和正弦值之间的关系也易错。
知识点
扫码查看完整答案与解析