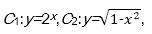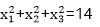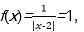函数零点的判断和求解
共205题

· 函数零点的判断和求解

函数零点的判断和求解
共205题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

1.方程的根的个数是(　　).

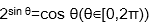
正确答案

解析

因为2sin θ>0,

所以cos θ>0,

令sin θ=x,-1≤x≤1,则问题转化为方程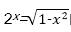的根的个数问题,

记

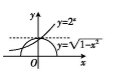
则问题又转化为两条曲线在x∈[-1,1]内交点个数的问题.

在同一坐标系中画出它们的图象,

如图所示

故选B.

知识点

函数零点的判断和求解

题型：填空题

填空题 · 5 分

7.方程()x-sin x=0在x∈[0,2π]内解的个数为　　　　.

正确答案

解析

　如图,方程在x∈[0,2π]内解的个数可以转化为函数与y=sin x在x∈[0,2π]内交点的个数

.根据图象可得交点个数为2,

即解的个数为2.

知识点

函数零点的判断和求解

题型：单选题

单选题 · 5 分

1.已知函数f(x)=sin(2ωx+)(ω>0)的相邻两条对称轴之间的距离为,将函数f(x)的图象向右平移个单位后,再将所有点的横坐标伸长为原来的2倍,得到g(x)的图象,若g(x)+k=0在x∈[0,]有且只有一个实数根,则k的取值范围是(　　).

A(-∞,]

B[-1,-)

C(-,]

D(-,]∪{-1}

正确答案

解析

因为f(x)相邻两条对称轴之间的距离为,结合三角函数的图象可知=.

又T==,所以ω=2,f(x)=sin(4x+).

将f(x)的图象向右平移个单位得到

f(x)=sin[4(x-)+]=sin(4x-)的图象,再将所有点的横坐标伸长为原来的2倍,得到g(x)=sin(2x-)的图象.

令2x-=t,因为x∈[0,],所以t∈[-,].

若g(x)+k=0在x∈[0,]有且只有一个实数根,

即y=sin t与y=-k在[-,]有且只有一个交点.

如图所示,由正弦函数的图象可知-≤-k<或-k=1,即-<k≤或k=-1

知识点

函数零点的判断和求解正弦函数的对称性函数y=Asin（ωx+φ）的图象变换

题型：单选题

单选题 · 5 分

6.设定义域为R的函数f(x)= 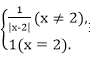若关于x的方程f2(x)+af(x)+b=0有3个不同的实数解x1,x2,x3,且x1<x2<x3,则下列说法中错误的是(　　).

B1+a+b=0

Cx1+x3=4

正确答案

解析

作出f(x)的图象(图略),

图象关于x=2对称,且当x=2时,

f(x)=1,故f(x)=1有三个不同实数根x,

除此之外,f(x)只有两个根或无根.

又f2(x)+af(x)+b=0有三个不同的实数

解x1<x2<x3,x2=2,

而x1+x3=2x2=4.又当x≠2时,

解得x1=1,x3=3,

故A,B,C正确.

知识点

函数的图象函数零点的判断和求解

题型：填空题

填空题 · 5 分

8.已知函数若存在x1,x2,当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)的取值范围是　　　　.

正确答案

解析

作出函数f(x)的图象如图,由图象可知,当时,

f(x1)=f(x2),

即

所以

令

由二次函数图象可知函数递增,

所以

即为x1f(x2)的取值范围.

知识点

函数零点的判断和求解

继续学习学习下一知识点

下一知识点 : 二次函数的零点问题

百度题库 > 高考 > 理科数学 > 函数零点的判断和求解

扫码查看完整答案与解析