函数零点的判断和求解
共205题

· 函数零点的判断和求解

函数零点的判断和求解
共205题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

已知是函数的两个零点，其中常数，设（）。

（1）用表示，;

（2）求证：;

（3）求证：对任意的，。

正确答案

见解析

解析

（1）由，。

因为，所以。

。 …………3分

（2）由，得

。

即，同理，。

所以。

所以。……………8分

（3）用数学归纳法证明。

（i）当时，由（Ⅰ）问知是整数，结论成立。

（ii）假设当（）时结论成立，即都是整数。

由，得。

即。

所以，。

所以。

即。

由都是整数，且，，所以也是整数。

即时，结论也成立。

由（i）（ii）可知，对于一切，的值都是整数。 ………13分

知识点

函数零点的判断和求解分析法的思考过程、特点及应用综合法的思考过程、特点及应用

题型：简答题

简答题 · 12 分

已知函数的振幅为2，其图象的相邻两个对称中心之间的距离为。

（1）若，求sina；

（2）将函数的图象向右平移个单位得到的图象，若函数

是在上有零点，求实数的取值范围。

正确答案

见解析。

解析

知识点

函数零点的判断和求解函数y=Asin（ωx+φ）的图象变换由y=Asin（ωx+φ）的部分图象确定其解析式

题型：填空题

填空题 · 4 分

已知函数是定义域为的偶函数. 当时，若关于的方程有且只有7个不同实数根，则实数的取值范围是　。

正确答案

解析

略

知识点

函数奇偶性的性质函数零点的判断和求解

题型：简答题

简答题 · 12 分

设，，若是函数的一个零点，且函数的最大值为。

（1）求实数和的值；

（2）中，设、、所对的边分别为、、，若，且，求的值。

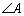
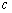
正确答案

见解析。

解析

（1），

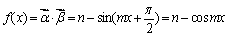
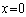
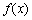
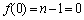
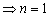
因为是的一个零点，即，，

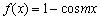
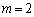
易知的最大值为，从而依题意有，综上，

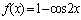
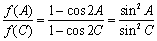
（2）由（Ⅰ）可知，于是，

由正弦定理及余弦定理有：，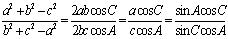

故，又，

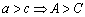
于是，

，即。

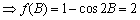
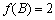
知识点

函数零点的判断和求解三角函数中的恒等变换应用正弦定理的应用三角函数的最值平面向量数量积的运算

题型：单选题

单选题 · 5 分

已知函数则函数的零点为

A和1

B和0

正确答案

解析

略

知识点

函数零点的判断和求解

继续学习学习下一知识点

下一知识点 : 二次函数的零点问题

百度题库 > 高考 > 理科数学 > 函数零点的判断和求解

扫码查看完整答案与解析