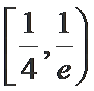- 函数零点的判断和求解
- 共205题
已知函数



22.求函数
23.已知关于



(1)求实数m的取值范围;
(2)证明:
正确答案
(Ⅰ) 
解析
(1)将






考查方向
解题思路
有函数的图象变化规律可得到函数的本来面貌,从而求得对称轴方程。
易错点
三角函数变换过程中参数的变换掌握不好,计算能力弱
正确答案
(Ⅱ)(1)
解析
(2)1)


依题意,




2)因为


所以

当
当
所以
考查方向
解题思路
结合函数图象,化简三角函数,然后建立不等关系,求出M的取值范围
易错点
计算能力弱,三角函数的图象变换和性质掌握不好,不会利用辅助角公式和诱导公式。
8.已知函数




正确答案
解析
由

所以
即






考查方向
解题思路
数形结合法来解答。
易错点
不知道怎么做。
知识点
14.若函数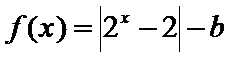
正确答案
(-2,+∞)
考查方向
易错点
1.不注意指数函数的有界性导致出错;
知识点
13.已知函数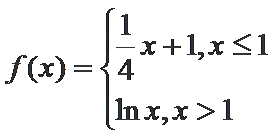
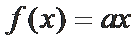
取值范围是___________
正确答案
解析
∵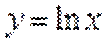
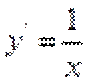
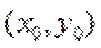
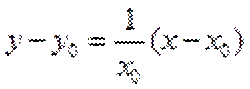
∴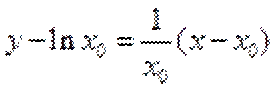
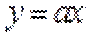
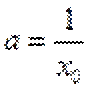
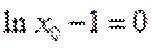
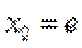
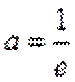
当直线与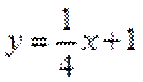
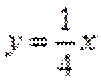
当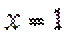
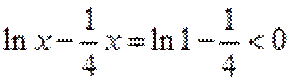
当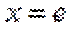
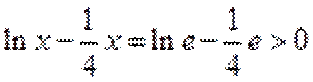
当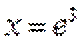
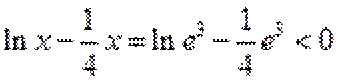
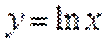
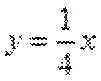
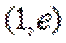
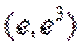
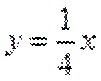
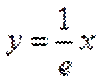
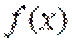
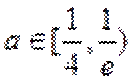
考查方向
解题思路
本题考查运用导数解决函数的能力,解题步骤如下: 先求导,找函数的切线方程,再利用零点的判定方法,找到a的取值范围。
易错点
本题必须注意审题,忽视则会出现错误。
知识点
已知函数

27. 讨论
28. 设曲线




29. 若关于


正确答案
(I) 当









解析
(I)解:由






下面分两种情况讨论:
(1)当
令


当


-
+
-
所以,




当


当


所以,


考查方向
解题思路
利用导数的运算、导数的几何意义解答。
易错点
不会分类讨论。
正确答案
(II)见解析;
解析
(II)证明:设点










由于















考查方向
解题思路
利用导数研究函数的性质、证明不等式等基础知识和方法.
易错点
不会利用导数的几何意义来解答。
正确答案
(III)见解析.
解析
(III)证明:不妨设








类似地,设曲线






设方程






由此可得
因为


所以,
考查方向
解题思路
分类讨论思想、函数思想和划归思想,综合分析问题和解决问题的能力。
易错点
难度大做不出来。
扫码查看完整答案与解析