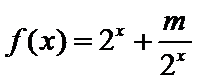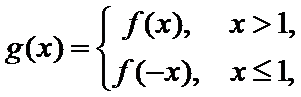- 函数零点的判断和求解
- 共205题
已知函数


25.如果函数



26.令


正确答案
(1)

当



当



解析
(Ⅰ)

令




所以



当




当



考查方向
解题思路
先求导后得到原函数的极值点后结合二次函数即可求得a的值,后面利用常用的方法求单调区间;
易错点
不理解函数

正确答案
(2)当


当

解析
(Ⅱ)
令







即函数





若





若










若

此时



若

当



故

若




又

所以

综上,当


当

考查方向
解题思路
按照判别式分类讨论各种情况下零点的个数。
易错点
不会确定分类的标准。
20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
21. 已知函数
(I)

(II)当



(III)若关于



正确答案
(1)1;
(2)2
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”.涉及对数函数,要特别注意函数的定义域.
(I)当

所以函数

又因为

(II)函数

当
令

所以

当


所以


当










而

当



所以



不合题意 综上可得
(III) 因为方程










由





∴


满足
两式相加得:




即证
设

则



∴

考查方向
解题思路
本题考查导数的性质,解题步骤如下:1、求导,然后解导数不等式,算极值。2、构造



易错点
1、第二问中的易丢对a的分类讨论。
2、第三问中构造函数不正确得不到正确结论。
知识点
19.已知函数


(1)求
(2)若对任意的


(3)若函数


正确答案
(1)
(2)
(3)
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”.涉及对数函数,要特别注意函数的定义域.
(1)由题意得


所以

(2)由(1)知

所以



又不等式整理可得

所以

当



同理,函数


综上所述,实数

(3)结论是
证明:由题意知函数

易得函数



因为



不妨令




即证

因为



综上所述,函数

考查方向
本题考查了利用导数的几何意义,利用导数求含参数的函数单调区间,分类讨论讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式,算极值。
2、对参数分类讨论求得单调区间。
3、涉及恒成立问题,转化成求函数的最值,利用“分离参数法”
易错点
1、第二问中恒成立问题,转化为求函数的最值,最值如何求解。
2、第三问中构造函数不正确得不到正确结论。
知识点
13.设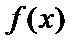
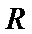
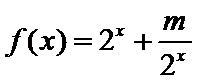
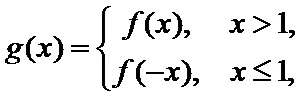
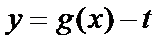
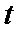
正确答案
解析
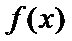
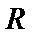
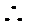
则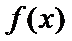
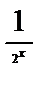
则当x>1时,函数为增函数,且当x
当x 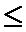


由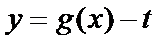
考查方向
解题思路
函数与方程的思想,将函数的零点转化为方程的解、两个函数的交点,用函数的图形来处理。
易错点
1、对零点概念、方程与函数的思想理解不到位,不能准确地转化为函数来处理。
2、本题不容易理解有且只有一个零点含义,从而造成求解上的不精确。。
知识点
12.若函数f(x)=

正确答案
解析
由f(x)=0知









考查方向
解题思路
把函数f(x)的零点问题转化为两个函数的交点问题,再利用函数的导数探究单调性,从而探索出两个函数的有三个交点时a的取值范围。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
难于构造出两个函数的交点问题。
知识点
已知函数
27.设
28.证明:存在




正确答案
当






解析
由已知,函数


所以
当


在区

当


解题思路
首先对函数




易错点
不会确定分类的标准导致出错或不分类;
正确答案
详见解析.
解析
由

令
则
故存在

令
由


所以
即
当

由(1)知,函数

故当


当


所以,当

综上所述,存在




考查方向
解题思路
要使得













因为










当



故当







易错点
找不到解决问题的思路导致无法入手。
15.若函数
正确答案
解析
∵当x=0时无零点,
考查方向
解题思路
1)对函数
2)当
3)讨论
4)借助单调性及其最值得出结论
易错点
本题易错在分类不清或者对单调性判断错误
知识点
10.已知定义在R上的奇函数y=f(x)的图像关于直线x=1对称,当-1≤x<0时,f(x)=-

正确答案
解析
根据性质做出图像
共有4个零点ABCD,且AB关于x=1对称
CD关于x=5对称
考查方向
解题思路
1)根据函数性质得出函数在(0,6)上的图像,
2)数形结合得到零点
3)根据对称性得出零点间关系
易错点
主要易错于函数图像不能有效的画出
知识点
11.已知函数


①当
②函数
③
④
其中正确命题个数是( )
正确答案
解析
因为f(x)为R上的奇函数,设x>0,-x<0,则



当


同理判断4正确,所以选B
考查方向
解题思路
根据函数的相关性质,结合子题目,依次判断
易错点
求导错误;
知识点
扫码查看完整答案与解析