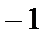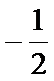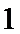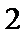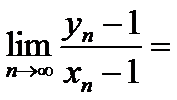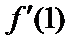- 数列的极限
- 共21题
14.无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意的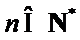
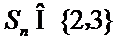
正确答案
解析
由于 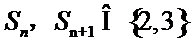
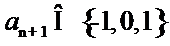
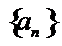
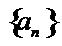
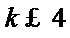
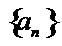
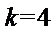
考查方向
解题思路
归纳,推理
易错点
推理的切入点
知识点
23.一青蛙从点





(1)若点




(2)若点




(3)若点





正确答案
(1)设
所以

(2)依题意,
随着

横向路程之和无限接近
所以 
(注:只要能说明横纵坐标的变化趋势,用文字表达也行)
(3)设点


其中

∴


∴
即当


又
∴当

∴

解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列




(1)能否唯一确定数列

(2)能否求得
(3)若





正确答案
(1)
即
由于

因此不能唯一确定数列
(2)为使
为使

∴ 


(3)

∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
12.若

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
23.若数列




已知数列



(1)求证:数列
(2)若

(3)当

正确答案
(1)因为
所以
所以数列
(2)
所以
当
设
则
当
设
则
因为
所以
即:
解得:
(3)当
则
当
当
即:
解析
解析已在路上飞奔,马上就到!
知识点
8.无穷数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设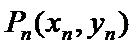
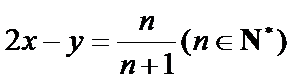
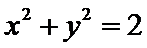
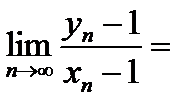
正确答案
解析
当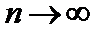
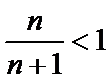
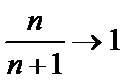
而由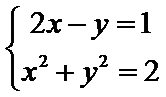
所以
而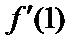
又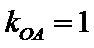
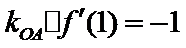
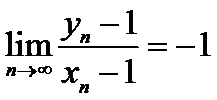
故选A.
知识点
5.设数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.将杨晖三角形中的每一个数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知公比为



(1)求数列


(2)对给定的




(3)设






正确答案
(1)依题意可知,
(2)由(1)知,






(3)






当





解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析