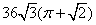- 空间几何体的三视图、表面积和体积
- 共1624题
一个圆锥的正（主）视图及其尺寸如图2所示，若一个平 行于圆锥底面的平面将此圆锥截成体积之比为l：7的上、下两部分，则截面的面积为。
A
B
C4π
正确答案
解析
：设小锥体的底面半径为r，大锥体的底面半径为3，利用一个锥体被平行于底面的截面所截得的小锥体与原锥体体积之比等于相似比的立方，
所以r=
截面的面积为
故选C。
知识点
在高三（1）班进行的演讲比赛中，共有5位选手参加，其中3位女生，2位男生.如果2位男生不能连续出场，且女生甲不能排在第一个，那么出场顺序的排法种数为
正确答案
解析
略
知识点
已知向量
正确答案
解析
因为向量
又
所以﹣1×（1+m）﹣1×2=0，
解得m=﹣3。
知识点
在复平面内，复数 对应的点位于（ ）
正确答案
解析
∵复数 
∴复数对应的点的坐标是（ 
∴复数 
故选A。
知识点
设随机变量
A3
B
C5
D
正确答案
解析
∵随机变量ξ服从正态分布N（3，4），
∵P（ξ＜2a﹣3）=P（ξ＞a+2），
∴2a﹣3与a+2关于x=3对称，
∴2a﹣3+a+2=6，
∴3a=7，
∴a=
故选A。
知识点
已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的全面积为
A
B
C
D
正确答案
解析
略
知识点
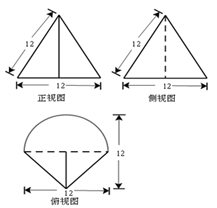
如图是某简单组合体的三视图，则该组合体的体积为 （ ）
A
B
C
D
正确答案
解析
由三视图知，几何体是一个简单的空间组合体，
前面是半个圆锥，圆锥的底面是半径为6的圆，母线长是12，
∴根据勾股定理知圆锥的高是6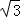
∴半个圆锥的体积是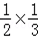
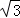
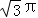
后面是一个三棱锥，三棱锥的底是边长为12、高为6的等腰三角形，三棱锥的高是6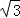
∴三棱锥的体积是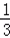
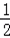
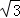
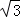
∴几何体的体积是36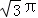
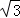
故选B。
知识点
如图圆
正确答案
解析
连接OC，∵PC是⊙O的切线，∴OC⊥PC，
又∵∠CPA=30°，R=3，
∴，
∴。
故答案为
知识点
已知
（1）求
（2）当
正确答案
见解析。
解析
（1）因为函数的周期为π，所以T=
因为函数图象上一个最低点为M（
所以﹣A+1=﹣1，所以A=2，
并且﹣1=2sin（2×
φ=2kπ﹣
因为
函数的解析式为：f（x）=2sin（2x+
（2）因为
sin（2x+
2sin（2x+
所以f（x）的值域为：
知识点
如图是一个几何体的三视图，若它的体积是3
A
B
C
D
正确答案
解析
由三视图可知此几何体为一个三棱柱，其直观图如图：底面三角形ABC为底边AB边长为2的三角形，AB边上的高为AM=a，侧棱AD⊥底面ABC，AD=3，
∴三棱柱ABC﹣DEF的体积V=S△ABC×AD=
∴a=
故选C。
知识点
扫码查看完整答案与解析