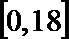- 简单的线性规划
- 共363题
7. 若


正确答案
知识点
5. 已知a,b>0,且a≠1,b≠1,若
正确答案
解析

当



当



考查方向
解题思路
分类讨论底数的范围,求出范围
易错点
对数函数的性质理解不够
知识点
5.若线性方程组的增广矩阵为




正确答案
16
解析
由题意,



考查方向
解题思路
线性方程组的增广矩阵是线性方程组另一种表示形式,明确其对应关系即可解决相应问题.即
易错点
矩阵与方程组的对应关系
知识点
14.若x,y满足约束条件
正确答案
8
解析
不等式组




考查方向
解题思路
线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合.
易错点
不等式组对应的平面区域的确定,确定z的最大值的位置.
知识点
8.设A={(x,y)|x2+(y-1)2=1},B={(x,y)|x+y+m≥0},则使A⊆B成立的实数m的取值范围是 。
正确答案
解析
集合A是圆x2+(y-1)2=1上的点的集合,集合B是不等式x+y+m≥0表示的平面区域内的点的集合,要使A⊆B,则应使圆被平面区域所包含(如图)
即直线x+y+m=0应与圆相切或相离(在圆的下方),当直线与圆相切时,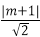
知识点
15.点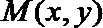
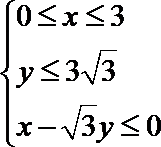
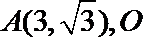
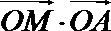
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若不等式

正确答案
解析
由题可知SM=2π,SN=48,则P=
考查方向
本题主要考查线性规划及几何概型。
解题思路
解题步骤如下:1、画出平面区域。2、利用概率公式求解.
易错点
本题必须注意利用图像完成。
知识点
14. 已知变量


正确答案
10
解析
如图所示,根据约束函数画出可行域,则A点为最大值,A(1,3)所以
考查方向
解题思路
先根据约束条件,作出正确的可行域
易错点
作图错误,找不到最大值的点
知识点
6. 若点


正确答案
解析
由题意知:



考查方向
本题考查了不等式与半平面的关系,在近几年的各省高考题出现的频率较低.
解题思路
点



易错点
审题失误,注意点不在区域内.
知识点
7.若关于

正确答案
解析
由图可知,当k=0或1时,刚好能构成等腰直角三角形,则面积为

考查方向
本题主要考查线性规划
解题思路
(1)表示平面区域;(2)求出区域面积,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示平面区域时发生错误。
知识点
扫码查看完整答案与解析