- 简单的线性规划
- 共363题
12. 若


正确答案
7
解析
画出可行域及直线


第12题图
考查方向
解题思路
掌握线性规划的计算方法,准确做出可行域,应用线性目标函数的讨论方法求解
易错点
可行域的求作,目标函数的几何意义。
知识点
7.已知



正确答案
解析
如下图所示,根据题意作出可行域,可知在(2,-1)处取最大值,所以2m-1=1,所以m=1
考查方向
解题思路
根据所给的约束条件,作出可行域,根据目标函数求函数最大值,进而求出m值
易错点
作图错误,找不到最大值
知识点
13.记集合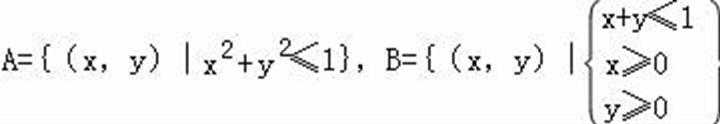
正确答案
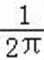
解析
由题意知,集合A表示的平面区域为以原点为圆心,1为半径的圆,其面积为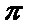
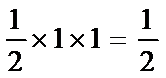
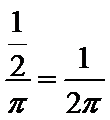
考查方向
解题思路
先求出集合A,B表示平面区域的面积,然后利用几何概型的概率公式求解即可。
易错点
不理解题中给出的条件是让求什么
知识点
7.平面内满足约束条件



正确答案
解析
画出可行域
由图可知平移2x+y=0,得到最小距离时经过点A(1,1),因为过点A的直线方程为2x+y-3=0,根据平行线之间的距离可得
考查方向
解题思路
1)画出可行域,标记2x+y=0
2)找到可行域到2x+y=0的最短距离,做平行线求最优解
3)根据对称性可知所求答案即最短距离的2倍
易错点
主要体现在①可行域不规范,②直线平移过程忽略直线的斜率,③题意理解错误
知识点
10.若不等式组

正确答案
解析
如图,

由于不等式组


再注意到直线


三角形,易知,

从而

化简得:




考查方向
解题思路
本题考查线性规划问题中的二元一次不等式组表示平面区域,利用已知条件将三角形的面积用含

易错点
本题属于中档题,注意运算的准确性及对结果的检验.
知识点
12.已知不等式组



正确答案
解析
出不等式表示的平面区域,如图所示,
即B(3,3),A(1,1),
故此题答案为
考查方向
解题思路
根据不等式组画平面区域,并找出(-1,0)点。过(-1,0)点转动直线与可行域有交点时找出最优解,从而得到
易错点
本题易在

知识点
14.若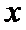

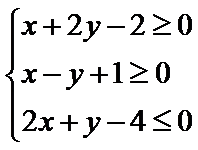
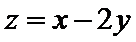
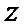
正确答案
[-3,2]
解析
有题意可知,作图可以知道,在点(2,0)处取最大值2,在点(1,2)处取最小值-3
考查方向
线性规划的简单应用
解题思路
先作出可行域,然后找到最值点,求出最值
易错点
作图错误,找点错误
知识点
14.某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
正确答案
16 29
解析
(1)由题意第一天与第二天都售出的有3种 所以第一天售出但第二天未售出的商品有19-3=16
(2)当商品种数最少时,应让这三天售出相同的种数最多 (用不同的数字代表不同的商品)
第一天:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
第二天:1 2 3 4 21 22 23 24 25 26 27 28 29
第三天:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
所以这三天售出的商品中相同的商品种数为29种
考查方向
解题思路
让第一天与第三天出售相同的商品种数最多
易错点
分清第一天与第三天出售相同商品的种数
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
扫码查看完整答案与解析
















