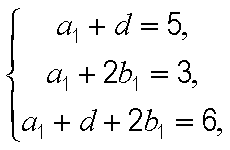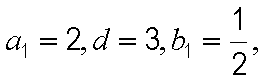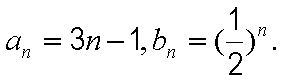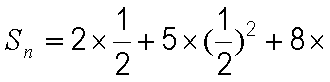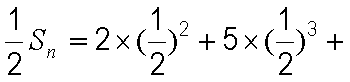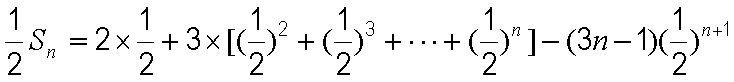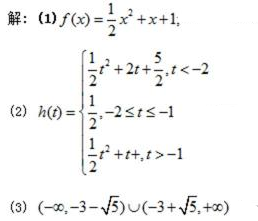- 二次函数与幂函数
- 共2034题
已知函数
(1)若


(2)若函数

(3)设函数




正确答案
见解析
解析
解析:(1)当










(2)
















(3)∵






①当

















②当






③当













知识点
已知极坐标的极点在平面直角坐标系的原点





(1)求点
(2)求点

正确答案
见解析
解析
(1)

所以点
(2)因为

所以


法一:由(1)点





法二:





知识点
等差数列
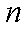
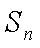
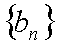
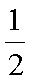
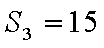
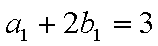
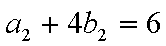
(1)求数列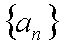
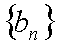
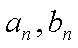
(2)求数列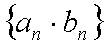
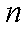
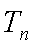
正确答案
见解析
解析
解析:
(1)设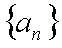
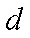
所以
解得
所以
(2)由(1)知
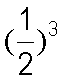
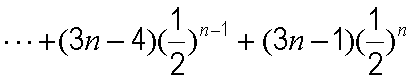
①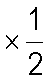
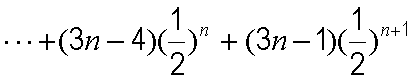
①-②得
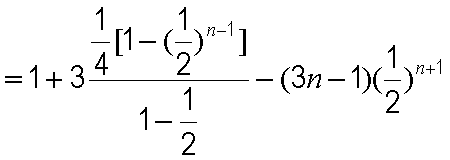
整理得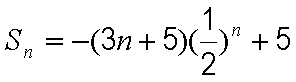
知识点
根据下列算法语句,将输出的A值依次分别记为a1,a2,…,an,…,a2 014
(1))求数列{an}的通项公式;
(2)令


正确答案
见解析
解析
(1)由已知,当n≥2时,

而
所以数列{

(2)由知
知识点
已知实数

(1) 若直线








(2) 当

命题意图:考查二次曲线的离心率,二次函数的最值,分类讨论思想,中档题。
正确答案
见解析。
解析
(1) 由


设
代入曲线方程:

因为





(2)记

①若
②若
知识点
10. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 设二次函数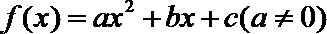
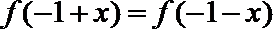
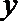
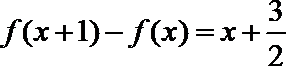
(1)求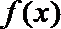
(2)若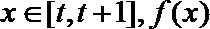
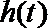
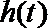
(3)若不等式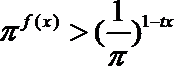
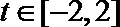
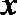
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设集合

正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
11.函数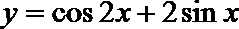
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析