- 二次函数与幂函数
- 共2034题
设P是函数


正确答案
解析


故
知识点
设
正确答案
解析
设


知识点
如图,锐角









正确答案
见解析。
解析
由圆



因为





所以
又
所以
由

知识点
在数列中,



(1)求


(2)设




正确答案
见解析
解析
(1)容易求得:

故可以猜想

(i) 显然当
(ii) 假设当




那么当
------------(6分)
即当


(2)
所以
-----------------------(11分)
所以只需要证明

所以对任意的自然数

知识点
设曲线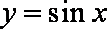
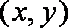
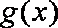
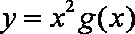
正确答案
解析
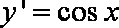
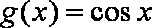
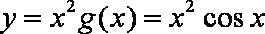
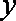
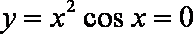
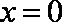
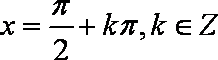
知识点
已知

正确答案
见解析。
解析
证法一:因为


所以
故
又3
所以原不等式成立,
证法二:因为



所以
同理
故
所以原不等式成立。
知识点
若实数x、y、z满足x2+y2+z2=2,则xy+yz+zx的取值范围是
正确答案
解析
∵xy+yz+zx≤x2+y2+z2=2,x=y=z,时等号成立;2(xy+yz+zx)=(x+y+z)2-( x2+y2+z2)≥-2,x+y+z=0时等号成立。∴-1≤xy+yz+zx≤2.
知识点
在斜三角形
(1)若

(2)若

正确答案
见解析
解析
解:(1)由正弦定理,得
从而

由余弦定理,得
整理得

(2)在斜三角形

所以

即
故
整理,得
因为△ABC是斜三角形,所以sinAcosAcosC
所以
知识点
已知数列







(1) 求数列
(2) 已知





正确答案
(1)
解析
解析:
(2)


知识点
若一元二次不等式f(x)>0的解集为{x|-2<x<1},则f(2x)<0的解集为
正确答案
解析
f(2x)<0

知识点
扫码查看完整答案与解析