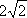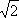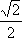向量的几何表示
共14题

· 向量的几何表示

向量的几何表示
共14题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

13.在中，点D满足，点是线段上的一个动点（不含端点），

若，则=______.

正确答案

解析

因为E在BD上

∴

考查方向

本题考查了平面向量的基本定理，三点共线原理的应用，属于基础题

解题思路

1、建立基底，所有的向量使用基底表示，2、使用共线条件得出关系

易错点

主要易错于三点共线的转换

知识点

向量的几何表示平面向量数量积的运算

题型：填空题

填空题 · 5 分

14．已知正方形ABCD的边长为2，E为CD的中点，则__________.

正确答案

解析

因为,所以

。

考查方向

本题主要考查向量数量积的运算以及向量的加减法。

解题思路

1)利用向量的加减法将已知向量转化为共线向量；

2)用向量数量积的定义计算。

易错点

本题易在用向量的加减法将向量转化为共线的向量时出现错误。

知识点

向量的几何表示

题型：单选题

单选题 · 5 分

8.如图，在等腰梯形中，，，，点，分别为，

的中点。如果对于常数，在等腰梯形的四条边上，有且只有个不同的点

使得成立，那么的取值范围是（）

A（，）

B（，）

C（，）

D（，）

正确答案

解析

以DC所在直线为x轴，DC的中垂线为y轴建立平面直角坐标系，则梯形的高为

考查方向

本题考查了平面向量的数量积运算，二次函数与二次方程的关系，分类讨论思想，属于中档题．

解题思路

该题使用建立坐标系，设P的坐标，根据得到关于x的方程，根据P的位置分四种情况讨论方程解得情况．

易错点

主要易错于讨论不全，漏解

知识点

向量的几何表示向量加减混合运算及其几何意义

题型：单选题

单选题 · 5 分

6.在平行四边形ABCD中，，点分别在边上，且，则=（）

正确答案

解析

,,所以，故选C选项。

考查方向

本题主要考查向量的线性运算和向量的数量积运算等知识，意在考查考生的运算求解能力和数形结合能力。

解题思路

1.先将向量,用基底表示出来；2.后利用数量积的运算法则求解即可。

易错点

不知道应该将向量,用基底表示出来；2.运算出错。

知识点

向量的几何表示向量的减法及其几何意义

题型：单选题

单选题 · 5 分

9. 如图，菱形的边长为2，,为的中点，若为菱形内任意一点（含边界），则的最大值为( )

正确答案

解析

由平面向量的数量积的几何意义知，等于与在方向上的投影之积,所以

考查方向

本题主要考查平面向量的数量积和向量的线性运算等知识，意在考查考生的转化与化归和运算求解能力.

解题思路

1.先将所求的函数的最大值的情况找到；2.利用平面向量基本定理将，后带入题中给出的数据计算即可。

易错点

1.不知道最大是什么情况；2.不会将所求的向量用已知的向量去表示。

知识点

向量的几何表示平面向量数量积的运算

题型：单选题

单选题 · 5 分

正方形ABCD的边长为1，=（）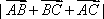

正确答案

解析

略

知识点

向量的几何表示

题型：单选题

单选题 · 5 分

设平面向量，，均为非零向量，则“”是“”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

略

知识点

向量的几何表示

题型：填空题

填空题 · 4 分

已知向量，且，则钝角等于。

正确答案

解析

略

知识点

向量的几何表示

题型：单选题

单选题 · 5 分

如右图,在△中, ,是上的一点,若,则实数的值为（）

正确答案

解析

略。

知识点

向量的几何表示

题型：单选题

单选题 · 5 分

4.如图，在的方格纸中，若起点和终点均在格点的向量满足，则（）

正确答案

解析

设方格边长为单位长.在直角坐标系内，，由得，所以，解得，所以，，选.

知识点

向量的几何表示

继续学习学习下一知识点

下一知识点 : 向量的模

百度题库 > 高考 > 理科数学 > 向量的几何表示

扫码查看完整答案与解析