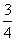- 两角和与差的余弦函数
- 共32题
设△ABC的内角A,B,C所对的边分别为a,b,c.若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则sinA∶sinB∶sinC为( )
正确答案
解析
由题意可设a=b+1,c=b-1.又∵3b=20a·cosA,∴3b=20(b+1)·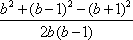
知识点
下列函数为奇函数的是( )
正确答案
解析



知识点
三角形



正确答案
解析
略
知识点
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆。
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值。
正确答案
见解析
解析
(1)因为CD为△ABC外接圆的切线,
所以∠DCB=∠A.
由题设知
故△CDB∽△AEF,所以∠DBC=∠EFA.
因为B,E,F,C四点共圆,
所以∠CFE=∠DBC,故∠EFA=∠CFE=90°。
所以∠CBA=90°,
因此CA是△ABC外接圆的直径。
(2)连结CE,因为∠CBE=90°,
所以过B,E,F,C四点的圆的直径为CE,
由DB=BE,有CE=DC,又BC2=DB·BA=2DB2,所以CA2=4DB2+BC2=6DB2.
而DC2=DB·DA=3DB2,故过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为
知识点
已知向量

正确答案
解析

知识点
一个六棱锥的体积为

正确答案
12
解析
设六棱锥的高为

则由体积



知识点
已知△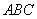
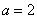
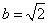
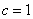
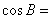
正确答案
解析
略
知识点
已知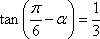
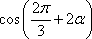
正确答案
解析
设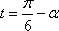
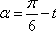
则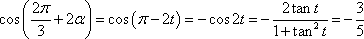
知识点
如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积。
正确答案
见解析
解析
(1)
证明:因为DE⊥EF,CF⊥EF,
所以四边形CDEF为矩形。
由GD=5,DE=4,得
由

在△EFG中,有EF2=GE2+FG2,
所以EG⊥GF.
又因为CF⊥EF,CF⊥FG,得CF⊥平面EFG,
所以CF⊥EG.
所以EG⊥平面CFG,即平面DEG⊥平面CFG.
(2)解:在平面EGF中,过点G作GH⊥EF于点H,
则
因为平面CDEF⊥平面EFG,得GH⊥平面CDEF,VCDEFG=
知识点
函数
正确答案
解析
略
知识点
扫码查看完整答案与解析