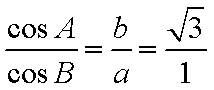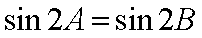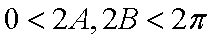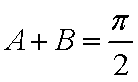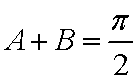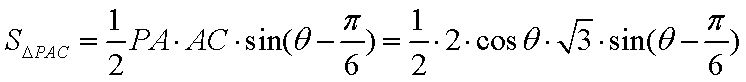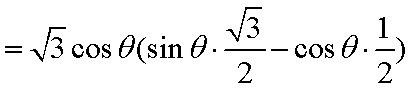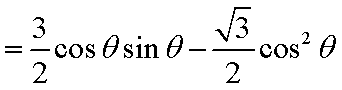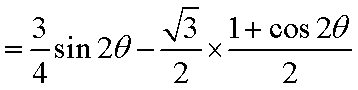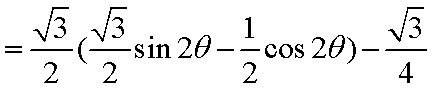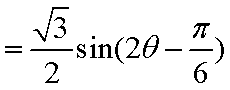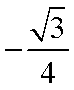- 正弦定理
- 共176题
1
题型:简答题
|
在









(1)求角
(2)若

正确答案
(1)
解析
解析:(1)



又



(2)









知识点
三角函数的化简求值三角函数中的恒等变换应用正弦定理数量积的坐标表达式
1
题型:简答题
|
在△








正确答案
见解析
解析
∵


又


在△


三角形面积
知识点
正弦定理
1
题型:简答题
|
已知△ABC中,角A、B、C的对边分别
(1)求
(2)求
正确答案
见解析。
解析
(1)
由余弦定理得
(2)由正弦定理知:
知识点
诱导公式的作用二倍角的余弦正弦定理余弦定理
1
题型:简答题
|
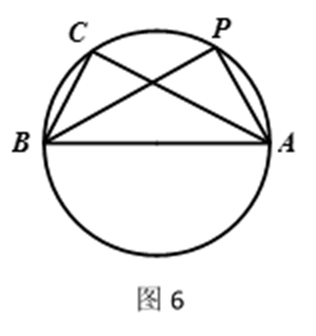
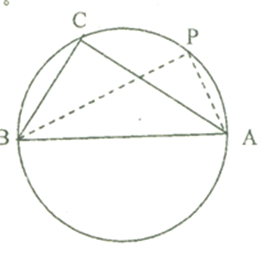
在
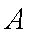
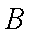
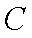
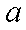
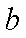

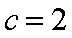
(1)求证: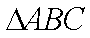
(2)如图6,设圆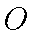
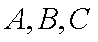
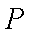
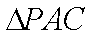
正确答案
见解析
解析
(1)证明:由正弦定理得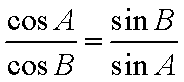
整理为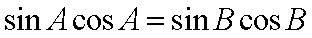
又因为
∴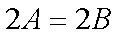
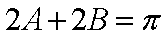
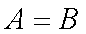
∵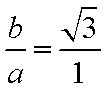
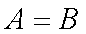
由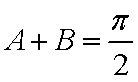
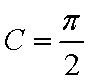
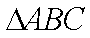
(2)由(1)及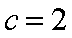
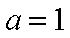
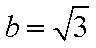
设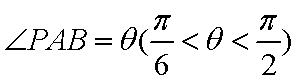
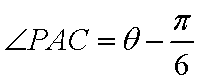
在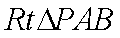
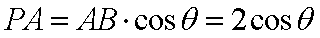
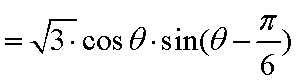
因为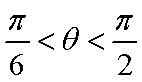
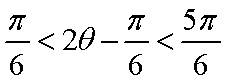
当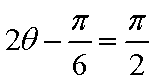
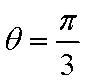
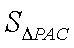
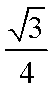
知识点
正弦定理
1
题型:简答题
|
在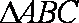
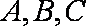
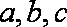
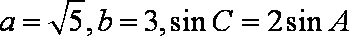
(1)求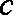
(2)求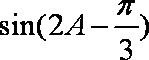
正确答案
见解析
解析
(1)由正弦定理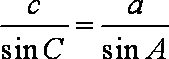
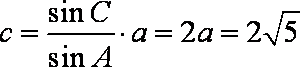

(2)由余弦定理,得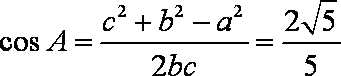

所以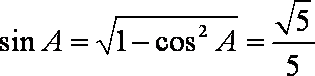
故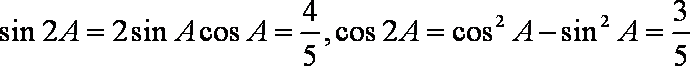
所以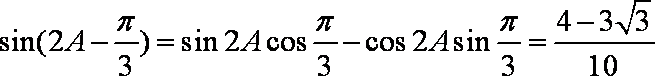
知识点
正弦定理
下一知识点 : 正弦定理的应用
扫码查看完整答案与解析