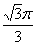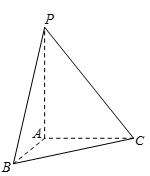- 旋转体(圆柱、圆锥、圆台)
- 共22题
若一个圆锥的侧面展开图是面积为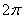
正确答案
解析
根据该圆锥的底面圆的半径为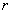
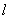
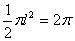
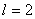
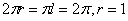
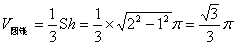
知识点
若圆锥的侧面积为

正确答案
解析
设圆锥的底面半径为




∴



知识点
若一个圆锥的侧面展开图是面积为
正确答案
解析
略
知识点
已知三棱锥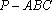
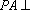
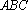
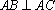
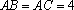
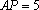
(1)求二面角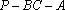
(2)把△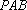
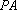
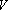
正确答案
见解析
解析
(1)解法一:设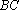
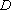
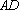
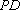
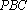
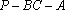
在等腰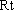
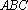
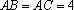
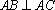
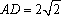
由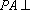
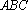
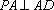
在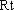
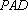
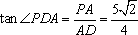
故二面角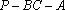
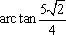
解法二:如图建立空间直角坐标系,可得各点的坐标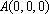
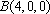
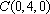
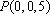
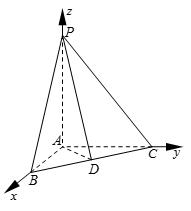
于是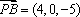
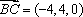
由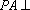
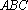
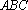
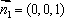
设
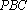
因为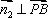
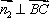
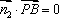
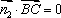
即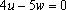
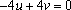
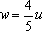

取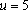
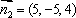
设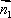
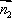
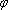
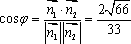
结合图可判别二面角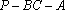
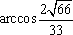
(2)由题设,所得几何体为圆锥,其底面半径为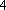

该圆锥的体积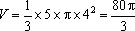
知识点
如图所示,一个空间几何体的正视图和左视图都是边长为

正确答案
解析
略
知识点
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________。
正确答案
解析

连接D1E1,过P点作PH垂直于底面A1B1C1D1,交D1E1于点H,
P点到直线CC1的距离就是C1H,
故当C1H垂直于D1E1时,P点到直线CC1距离最小,
此时,在Rt△D1C1E1中,C1H⊥D1E1,D1E1·C1H=C1D1·C1E1,∴C1H=
知识点
若一个圆锥的侧面展开图是面积为
正确答案
解析
略
知识点
某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为
正确答案
解析
由三视图可知,该几何体是三分之一个圆锥,其体积为:
知识点
8.侧面展开图是半径长为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,圆锥的顶点是






(1)计算圆锥的侧面积;
(2)求

正确答案
(1)
所以,
(2)


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析