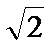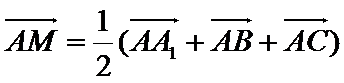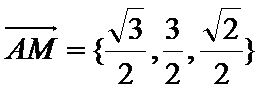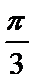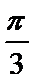- 旋转体(圆柱、圆锥、圆台)
- 共22题
8.圆锥的侧面展开图是圆心角为π,面积为2π的扇形,则圆锥的体积是___________
正确答案
解析
2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
考查方向
解题思路
本题考查运用圆锥侧面积求底面半径及母线,再求高,进而求体积。解题步骤如下:2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
易错点
本题必须注意审题,忽视则会出现错误。
知识点
6.如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
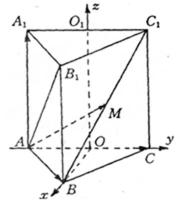
18.已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
(1)求正三棱柱的侧棱长.
(2)若M为BC1的中点,试用基向量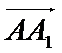
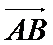
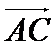
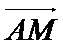
(3)求异面直线AM与BC所成角.
正确答案
(1)设侧棱长为b,则A(0,-1,0), B1(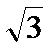
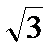
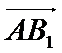
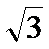
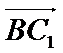
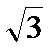
∵ AB1 ⊥AB1
∴ -3+1+b2=0, b=
(2)
(3) 设异面直线AM与BC所成角为α,
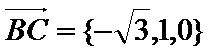
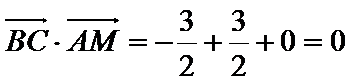
∴ α=900
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
(1)求出r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,求最省时
正确答案
解:(1)设圆锥纸筒的容积为

由该圆锥纸筒的容积为π,则

故r与h满足的关系式为
(2)工厂要求制作该纸筒的材料最省,即所用材料的面积最小,即要该圆锥的侧面积最小
设该纸筒的侧面积为



所以

设

由

当



因此,


由


解析
解析已在路上飞奔,马上就到!
知识点
8.圆锥的侧面展开图是圆心角为π,面积为2π的扇形,则圆锥的体积是___________
正确答案
解析
2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
考查方向
解题思路
本题考查运用圆锥侧面积求底面半径及母线,再求高,进而求体积。解题步骤如下:2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
易错点
本题必须注意审题,忽视则会出现错误。
知识点
8.如图,有一圆柱开口容器(下表面封闭),其轴截面是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒的所经过的最短路程是( )
正确答案
解析
如图,把圆柱侧面展开得








考查方向
解题思路
把圆柱侧面展开得



易错点
本题易在思路的寻找上迷失。
知识点
6.若圆锥的侧面积与过轴的截面面积之比为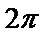
正确答案
解析
由题意得: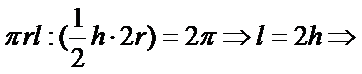
知识点
13.有一个几何体的三视图及其尺寸如下(单位
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
等腰直角三角形的直角边长为1,则绕斜边旋转一周所形成的几何体的体积为 .
正确答案
解析
由已知得出几何体为圆锥,底面积为

考查方向
本题主要考查了旋转体的概念以及旋转体的体积
易错点
旋转体以谁为旋转轴直接导致图形的不同,是容易出错的
知识点
(4分)(2015•上海)若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为 .
正确答案
知识点
扫码查看完整答案与解析