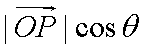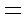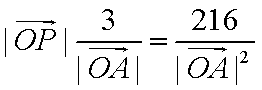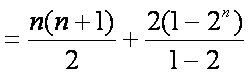- 复合函数的单调性
- 共281题
某几何体的三视图如题（7）图所示，其侧视图是一个边长为l的等边三角形，俯视图是两个正三角形拼成，则此几何体的体积为
A1
B
C
D
正确答案
解析
由几何体的三视图可知：此几何体是两个相同的三棱锥拼接而成的，由侧视图知三棱锥的高为
知识点
执行如图所示的程序框图，若输出
A
B
C
D
正确答案
解析
解析：程序在运行过程中各变量的值如下表示：
是否继续循环 S n
循环前 / 0 1
第一圈 是 1 2
第二圈 是 3 4
第三圈 是 7 8
第四圈 是 15 16，
因为输出：S=15。
所以判断框内可填写“n＞8”，
故选：B
知识点
执行如图所示的框图，若输入
正确答案
解析
略
知识点
在平面直角坐标系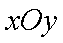
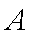
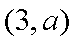
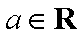
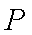
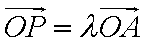
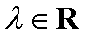
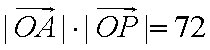
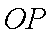
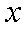
正确答案
24
解析
点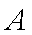
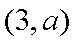
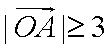
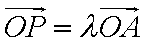
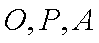
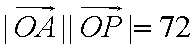
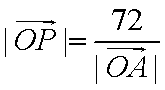
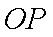
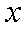
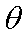
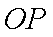
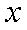
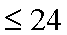
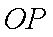
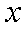
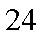
知识点
若圆柱的侧面积和体积的值都是
正确答案
3
解析
略
知识点
已知数列{an}，{bn}满足：a1b1＋a2b2＋a3b3＋…＋anbn＝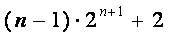
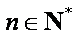
（1）若{bn }是首项为1，公比为2等比数列，求数列{an}的通项公式；
（2）在数列{an}中，a1＝1，对任意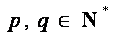
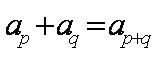
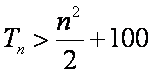
正确答案
见解析。
解析
（1）因为a1b
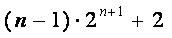
则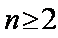
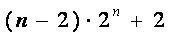
两式相减，得anbn＝n·2n(n≥2)，
当n＝1时，a1b1＝2，满足上式，所以anbn＝n·2n(nN*)，
又因为{bn }是首项为1，公比为2的等比数列，则bn＝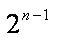
所以an＝2n。
（2）因为对任意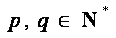
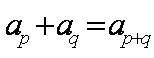
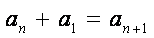
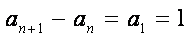
所以数列{an}是首项为1，公差为1的等差数列，所以an＝n，·
由（1）得bn＝2n，
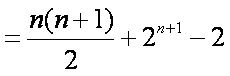
不等式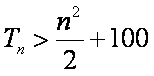
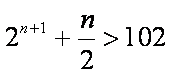
所以，满足条件的自然数n的最小值为6。
知识点
若在由正整数构成的无穷数列
正确答案
45
解析
解析：∵对任意的正整数k，该数列中恰有2k-1个k，
∴数列是1；2，2，2；3，3，3，3，3，…
设
1+3+5+…+（2n-1）=n2＜2014，解得n＜45
∴, 
所以
故答案为：45
知识点
在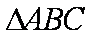
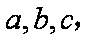
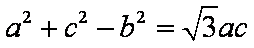
A
B
C
D
正确答案
解析
略
知识点
下列函数中，既是奇函数又在区间
A
B
C
D
正确答案
解析
略
知识点
设椭圆
（1）求椭圆
（2）设
正确答案
（1）
解析
（1）由题意可知B（0，-1），则A（0，-2），故b=2。
令y=0得
所以
（2）设N（
代入椭圆方程整理得：
故
设点M到直线PQ的距离为d，则
所以，
当
综上可知，
知识点
扫码查看完整答案与解析