- 复合函数的单调性
- 共281题
调查某电脑公司的三名产品推销员,其工作年限与年推销金额数据如表:由表中数据算出线性回归方程

正确答案
3
解析
由条件可知




知识点
已知函数
(1)求曲线

(2)若




(ⅰ)求
(ⅱ)若点

正确答案
见解析
解析
(1)



处的切线方程为

(2)(ⅰ)对于

当



当




∴
所以



(ⅱ)若


从而得

若



由上可得点



从而



知识点
甲、乙、丙、丁四人排成一行,则甲、乙都不在两边的概率为
正确答案
解析
甲、乙、丙、丁四人站成一排有如下24种情形:
甲乙丙丁、甲乙丁丙、甲丙乙丁、甲丙丁乙、甲丁乙丙、甲丁丙乙、
乙甲丙丁、乙甲丁丙、乙丙甲丁、乙丁甲丙、乙丁丙甲、乙丙丁甲、
丙甲乙丁、丙甲丁乙、丙乙甲丁、丙乙丁甲、丙乙丁甲、丙丁乙甲、
丁甲乙丙、丁甲丙乙、丁乙甲丙、丁乙丙甲、丁丙甲乙、丁丙乙甲.
其中甲、乙都不在两边有如下4种情形:
丙甲乙丁、丙乙甲丁、丁甲乙丙、丁乙甲丙.
因此所求概率为
知识点
函数




(1)若


(2)求证:当
正确答案
见解析
解析
(1)∵




∴
当



∴

又

∴ 
故实数

(2)
即为
令
再令
∵



∴
∴

∴


令
∵



∴

所以

知识点
已知






(1) 求椭圆的方程;
(2)若






正确答案
(1)
(2)
解析
(1)由几何性质可知:当
即

由
又

综上得
又由


经计算得


故椭圆方程为
(2)①当直线



②当直线


由 


代入弦长公式得:
同理由


代入弦长公式得:
所以
令


由①②可知,

知识点
已知集合A={x∈R||x|≥2},B={x∈R|x2﹣x﹣2<0}且R为实数集,则下列结论正确的是( )
正确答案
解析
集合A={x∈R||x|≥2}={x∈R|x≥2或x≤﹣2},B={x∈R|x2﹣x﹣2<0}={x∈R|﹣1<x<2}。
所以A∪B={x∈R|x>﹣1或x≤﹣2},所以A错误。
所以A∩B=∅,所以B错误。
∁RB={x∈R|x≥2或x≤﹣1},所以A⊆(∁RB),所以C正确,D错误。
故选C。
知识点
等差数列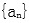
(1)求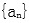
(2)设
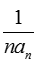
正确答案
见解析
解析
(1)设等差数列{an}的公差为d,则an=a1+(n-1)d.
因为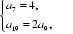
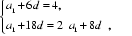
解得a1=1,d=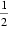
所以{an}的通项公式为an=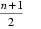
(2)因为bn=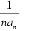
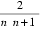
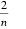
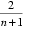
所以Sn=(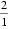
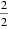
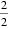
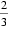
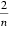
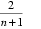
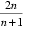
知识点
四棱锥




正确答案
解析
由题意可知四棱锥











知识点
已知椭圆


(1)求椭圆
(2)设直线








正确答案
见解析。
解析
(1)依题意可得

所以椭圆

(2)由



设




经过点

令

又


这说明直线


知识点
给出下列5种说法:
①在频率分布直方图中,众数左边和右边的直方图的面积相等;②标准差越小,样本数据的波动也越小;③回归分析就是研究两个相关事件的独立性;④在回归分析中,预报变量是由解释变量和随机误差共同确定的;⑤相关指数

其中说法正确的是
正确答案
②④⑤
解析
由统计学的相关定义可知,②④⑤的说法正确.
知识点
扫码查看完整答案与解析