- 复合函数的单调性
- 共281题
调查某电脑公司的三名产品推销员,其工作年限与年推销金额数据如表:由表中数据算出线性回归方程

正确答案
3
解析
由条件可知




知识点
甲、乙、丙、丁四人排成一行,则甲、乙都不在两边的概率为
正确答案
解析
甲、乙、丙、丁四人站成一排有如下24种情形:
甲乙丙丁、甲乙丁丙、甲丙乙丁、甲丙丁乙、甲丁乙丙、甲丁丙乙、
乙甲丙丁、乙甲丁丙、乙丙甲丁、乙丁甲丙、乙丁丙甲、乙丙丁甲、
丙甲乙丁、丙甲丁乙、丙乙甲丁、丙乙丁甲、丙乙丁甲、丙丁乙甲、
丁甲乙丙、丁甲丙乙、丁乙甲丙、丁乙丙甲、丁丙甲乙、丁丙乙甲.
其中甲、乙都不在两边有如下4种情形:
丙甲乙丁、丙乙甲丁、丁甲乙丙、丁乙甲丙.
因此所求概率为
知识点
函数




(1)若


(2)求证:当
正确答案
见解析
解析
(1)∵




∴
当



∴

又

∴ 
故实数

(2)
即为
令
再令
∵



∴
∴

∴


令
∵



∴

所以

知识点
等差数列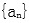
(1)求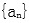
(2)设
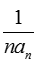
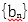
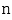
正确答案
见解析
解析
(1)设等差数列{an}的公差为d,则an=a1+(n-1)d.
因为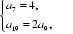
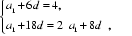
解得a1=1,d=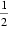
所以{an}的通项公式为an=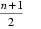
(2)因为bn=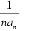
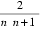
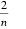
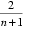
所以Sn=(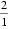
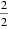
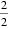
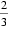
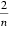
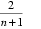
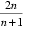
知识点
四棱锥




正确答案
解析
由题意可知四棱锥











知识点
扫码查看完整答案与解析