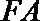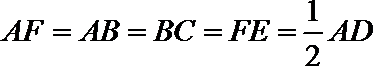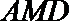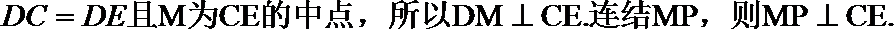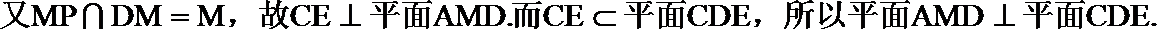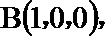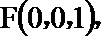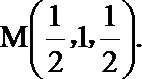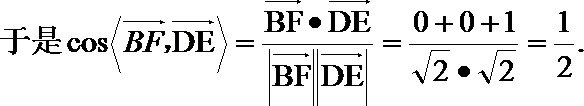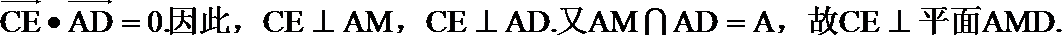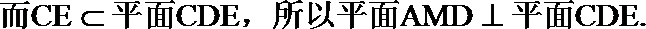- 复合函数的单调性
- 共281题
15.函数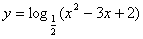
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
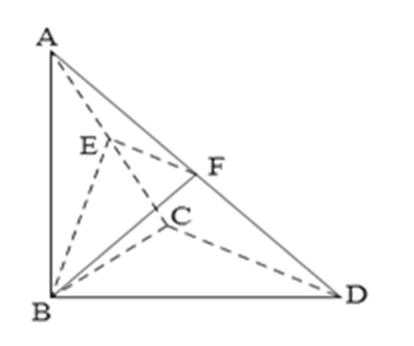
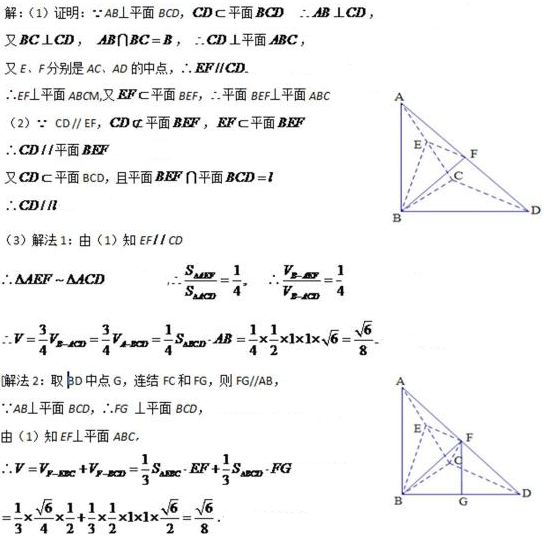
18.如图,已知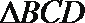
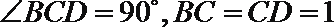
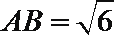


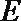
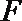
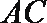
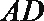
(1)求证:平面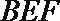
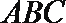
(2)设平面
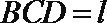
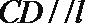
(3)求四棱锥B-CDFE的体积V.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.共有400辆汽车通过某一段公路时的速度如下图所示,则速度在
正确答案
320
解析
解析已在路上飞奔,马上就到!
知识点
4.在等比数列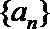
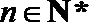
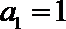
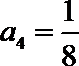
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
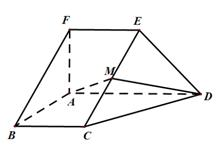
19.如图,在五面体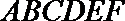
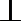
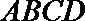
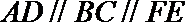
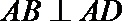
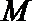
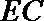
(I)求异面直线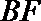
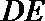
(II)证明平面
正确答案
方法一:
(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其补角)为异面直线BF与DE所成的角。
设P为AD的中点,连结EP,PC。
因为FE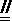

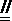
又FA⊥平面ABCD,所以EP⊥平面ABCD。
而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。
由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=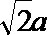
所以异面直线BF与DE所成的角的大小为60°
(II)证明:因为
方法二:建立空间直角坐标系,
点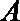
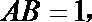
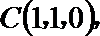
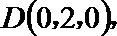
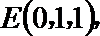
(I)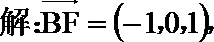
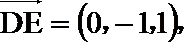
所以异面直线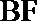
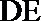
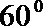
(II)证明: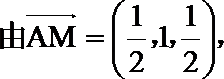
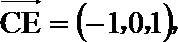
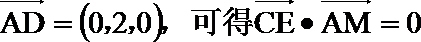
解析
解析已在路上飞奔,马上就到!
知识点
22.选考题(请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分。)
22、已知







(Ⅰ)求证:

(Ⅱ)若

23、已知曲线





(Ⅰ)化

(Ⅱ)若








24、已知

(Ⅰ)
(Ⅱ)
正确答案
22
证:(Ⅰ)








(Ⅱ)由(1)知
又
又





23
(Ⅰ)




(Ⅱ)当










24
(Ⅰ)

(Ⅱ)





解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数


(Ⅰ)求
(Ⅱ)若方程




(Ⅲ)令










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析