- 复合函数的单调性
- 共281题
某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格,某校随机抽取20位学生参加社区服务的数据,按时间段
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率。
正确答案
(1)6
(2)
解析
(1)由题意可知,
参加社区服务在时间段

参加社区服务在时间段

所以参加社区服务时间不少于90小时的学生人数为
………5分
(2)设所选学生的参加服务时间在同一时间段内为事件
由(1)可知,
参加社区服务在时间段

参加社区服务在时间段

从这6人中任意选取2人有
共15种情况。
事件

所以所选学生的服务时间在同一时间段内的概率
知识点
已知集合


正确答案
解析
略
知识点
已知正项数列



(1)求数列
(2)设


(3)设



正确答案
见解析。
解析
(1)法一:由
当


当



∵正项数列
∴
∴


∴ 
∴ 
法二:
当


由

当
∴ 
∵正项数列

∴ 
∴


∴ 
(2)
∴
∴
∴两式相减得
∵ 
∵
∴
(3)∵ 不等正整数
∴ 
∴ 
又
∴
故实数

知识点
定义在



正确答案
解析
略
知识点
某单位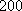
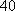
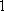
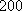
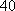
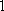

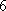
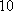
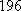
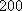

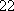

正确答案
37;20
解析
略
知识点
已知向量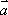
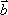
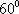
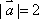
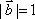
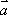
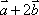
正确答案
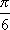
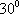
解析
略
知识点
对于函数
正确答案
解析
略
知识点
已知函数


(1)当


(2)求函数
(3)当


正确答案
(1)
(2)








(3)
解析
(1)

当

依题意


把


则曲线


(2)函数


(1)若
当


当



(2)若
当



当


综上所述,









…………………,9分
(3)当













另解:(1)当


(2)当







解得
综上所述,
知识点
已知双曲线C:


(1)求椭圆E的方程;
(2)若点P为椭圆的左顶点,

(3)若点P满足|PA|=|PB|,求证
正确答案
见解析。
解析
知识点
设复数



正确答案
解析
略
知识点
扫码查看完整答案与解析