- 复合函数的单调性
- 共281题
在复平面内,复数
正确答案
解析
略
知识点
已知函数

正确答案
解析
略
知识点
如图,在直三棱柱




(1)求异面直线

(2)若



正确答案
见解析。
解析
解法一:
(1)取




∴


设


∴
∵在

∴异面直线


(2)由(1)知,
因为三棱柱


又∵

∴



即



连结







又∵平面



而



由

即二面角

∴所求二面角

解法二:
(1)如图分别以





系
设





∴
∴
∴异面直线


(2)设

由


∴
设平面

则

∴


易知平面

∴
∴二面角

知识点
已知函数




①函数
②函数
③当

④如果当


其中正确命题的序号是(写出所有正确命题的序号)
正确答案
①②③
解析
略。
知识点
设数列



(1)求数列
(2)对一切

(3)记数列




正确答案
见解析。
解析
(1)由

即数列



(2)∵
∴要证明

即证

构造函数
则




减,故
∴


∴
(3)∵

∴
利用错位相减求得:
∴
知识点
已知函数

a=(20.2)·


正确答案
解析
略
知识点
已知点(1,2)是函数


(1)求数列
(2)将数列

正确答案
见解析。
解析
(1)把点(1,2)代入函数


当

当

经验证可知

(2)由(1)知数列


∴此数列的和为
又数列

∴所求剩余项的和为
知识点
已知F1,F2是椭圆C: 


(1)求椭圆C的方程。
(2)椭圆C上任一动点M
正确答案
见解析。
解析
(1)由已知,点P
∴有
又
∴M为P、F2的中点,┉┉┉┉┉┉┉┉2分
∴
∴由
解①②,解得

∴
故所求椭圆C的方程为
(2)∵点


∴
解得
∴
∵点P



即
知识点
函数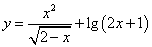
正确答案
解析
略
知识点
设函数
(1)求
(2)若



正确答案
见解析。
解析
(1)由已知
当



当



由


∴


(2)当
∴
令
则


∵

∴


…………………………………(11分)
又∵


知识点
扫码查看完整答案与解析